第十章  习题

第一节　回归与相关分析　(64)

单选题 

1.    研究一个(或多个)数值自变量的变化如何影响数值因变量的分析为：

A．回归分析  B. 相关分析 C. 秩分析 D. 独立性分析

2.    研究两个数值变量的相关程度的分析为：

A．回归分析  B. 相关分析 C. 秩分析 D. 独立性分析

3.    相关分析是：

A、研究变量之间的变动关系       

B、研究变量之间的数量关系

C、研究变量之间相互关系的密切程度

D、研究变量之间的因果关系

4.    回归这个术语是由英国著名统计学家F.Galton在19世纪末期研究孩子及他们父母的身高时提出来的，F.Galton给出的回归效应的含义是：

A．孩子的身高值与父母的身高值在一条直线附近

B. 孩子的身高值与父母的身高值相关

C. 孩子们的身高值向中间值靠近

D. 以上皆不对

5.    收集了n组数据(xi，yi)，i=1，2，……，n，为了解变量x与y间是否有相关关系，可以从下列那种图形加以考察？

  A. 直方图  　B.　散点图 　 C. 正态钟形曲线  D. 点线图

6.    收集了n组数据(xi，yi)，i=1，2，……，n，画出散点图，若n个点基本在一条直线附近时，称这两变量间具有：

A．独立的关系  　  B. 不相容的关系

C. 函数关系  　　  D. 线性相关关系

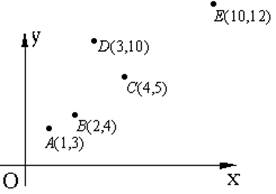
7.    有5组 (xi，yi)资料如图10.1所示。则去掉哪一点后，剩下的4组数据的相关系数最大? 

A．B点  B．C点  C. D点  D.E点                           

 

 

 

 

 

图10.1　

8.    在作散点图时，图中的点从左下角到右上角有明显的直线趋势，这时可以认为这两个变量

   A．负相关  B.正相关  C.不相关  D. 无法确定

9.    相关系数的取值范围是:
     A、-1≤ｒ≤0           B、0≤ｒ≤1
     C、-1≤ｒ≤1           D、-1<ｒ<1

10.              在变量x和变量y的直线相关分析中,|r|值越大,则：

A. 各散点越靠近直线              B. 各散点越离开直线

C. 直线越靠近x轴                D. 直线越远离x轴

11.              当相关系数r=0时,说明变量x与变量y：

A.不存在任何关系         B.存在相关关系的可能性很小

C.关系不能确定           D.不存在直线关系,但不排除存在某种曲线关系

12.              如果两个变量之间的相在系数为–1，这说明两个变量之间是

  A、完全相关    B、低度相关     C、中度相关  D、不相关

13.              若物价上涨,商品的需求量相应减少,则物价与商品需求量之间的关系为：

A. 不相关     B. 负相关    C. 正相关      D. 曲线相关

14.              当一个现象的数量由小变大，而另一个现象的数量相反地由大变小时，这种相关关系称为

A、线性相关    B、非线性相关    C、正相关    D、负相关

15.              有学生十人(甲、乙、……、癸), 他们期终考的数学成绩与该学期数学课的缺课数，如下表10.1所示。

　　　　　　　　　　　　　　　　表10.1

学 生

 甲

 乙

 丙

 丁

 戊

 己

 庚

 辛

 壬

 癸

缺课数

  1

  2

  3

  3

  4

  3

  5

  6

  3

  0

成 绩

 100

 90

 90

 80

 70

 70

 60

 60

 80

 100

设两者的相关系数为r, 则有：

   A． -1≤ｒ≤-0.6               B．   0.6<ｒ<1

  C． -0.1≤ｒ≤0.2    　　D．   0.2<ｒ<0.6

16.              如果散点图没有表示出变量x与y具有线性关系，而是具有某种曲线关系，此时：

   A．可以作回归分析 

B. 肯定不能作回归分析

C. 不能够直接做回归分析，一般首先要做数学转换 

D. 无法确定

17.              相关分析与回归分析，在是否需要确定自变量和因变量的问题上：

A、前者勿需确定，后者需要确定    B、前者需要确定，后者勿需确定

C、两者均需确定                   D、两者都勿需确定

18.              如果两个变量x、y具有线性关系y＝-8x，则对这两个变量的相关系数r＝：

  A．－1/8         B.1/8          C.1         D.-1

19.              两个变量的直线回归方程中，若回归系数为负，则：

A、表明两个变量正相关     B、表明两个变量负相关

  C、表明相关程度很弱       D、不能说明相关的方向和程度

20.              简单回归分析是指：

  A．计算简单的回归分析

B．自变量是虚拟变量的回归分析

C．因变量是虚拟变量的回归分析

D．两个变量的回归分析

21.              在计算回归直线时，科学常用的方法是：

A．画图法  B. 最小二乘法  C. 试验法　 D.　以上皆不是

22.              在回归直线方程＝a＋bx中,b表示：

A. 当x增加一个单位时,y的精确增加量

B. 当y增加一个单位时,x的精确增加量

C. 当x增加一个单位时,y的平均增加量

D. 当y增加一个单位时, x的平均增加量

23.              对于回归直线＝9x＋100，若x每增加一个单位，则y平均增加

A、100个单位       B、109个单位 

  C、9个单位       　D、91个单位

24.              已知某工厂甲产品产量和生产成本有直线关系，在这条直线上，当产量为1000时，其生产成本为30000元，其中不随产量变化的成本为6000元，则成本总额对产量的回归方程是：

A、     B、   

  C、     D、

25.              某校对学生的考试成绩和学习时间的关系进行测定,建立了考试成绩倚学习时间的直线回归方程为: =180-5x,其中该学校考试成绩满分为100分，学习时间的单位为小时，这个方程明显有误,错误在于：

A. a值的计算有误,b值是对的

B. b值的计算有误,a值是对的

C. a值和b值的计算都有误

D. 自变量和因变量的关系搞错了

26.              设变量x与变量y的总体相关系数为ρ，在一次随机抽样中，计算得到样本的相关系数r，下面有关ρ和r叙述不正确的是：

A. 若ρ=0.6，有可能r<0

B. r是ρ的点估计

C. 若r>0表示样本中y和x正相关，r<0表示负相关

D. 若ρ=0，则必有r=0

27.              在双变量(x，y)的相关与回归分析中有:

A. r值与b值的符号相同              B．r值与b值毫无关系

C．|r|值越大|b|值越大               D．|r|值越大|b|值越小

28.              在简单回归分析中，在由样本对总体进行推断时，要计算t统计量的值，那么t统计量的自由度为：
    A、n           B、n－2           C、n－1           D、n－2－1

多选题

1.    讨论两个数值变量之间关系常用的统计分析方法是：

  A．c2分析  B.秩方法  C.回归分析  D. 方差分析  E. 相关分析

2.    相关系数r = 0说明所分析的两个变量之间:

A．肯定不线性相关      B．肯定不曲线相关    C．可能完全不相关

D．可能是曲线相关      E．可能不线性相关

3.    下列属于正相关的现象是：

A.家庭收入越多,其消费支出也越多

B.某产品产量随工人劳动生产率的提高而增加

C.流通费用率随商品销售额的增加而减少

D.生产单位产品所耗工时随劳动生产率的提高而减少

E.产品产量随生产用固定资产价值的减少而减少

4.    下列哪些关系是相关关系:

A.家庭收入多少与消费支出增长的关系

B.农作物收获和施肥量的关系

C.商品销售额和利润率的关系

D.产品产量与单位成品成本的关系

5.    下列属于负相关的现象是:

A.商品流转的规模愈大,流通费用水平越低

B.流通费用率随商品销售额的增加而减少

C.国民收入随投资额的增加而增长

D.生产单位产品所耗工时随劳动生产率的提高而减少

E.某产品产量随工人劳动生产率的提高而增加

6.    相关分析中的负相关是指:

A、自变量数值增加，因变量数值也增加     

B、自变量数值增加，因变量数值相应减少

C、自变量数值减少，因变量数值也减少

D、自变量数值减少，因变量数值相应增加

E、自变量数值增加，因变量数值不变

7.    相关系数是零,说明两个变量之间的关系：

A. 高度相关       B. 完全不相关      C.低度相关

D.不相关          E. 中度相关

8.    若两个变量之间的相关系数为-1,则这两个变量是：

A. 正相关关系         B. 负相关关系      C.不相关

D.不完全相关关系      E.完全相关关系

9.    直线相关分析的特点有：

A、两变量不是对等的     B、两变量只能算出一个相关系数

C、相关系数有正负号     D、相关系数的绝对值是介于0~1之间的数

10.              下列关于相关系数r说法正确的是

 A、r2 表示因变量的变异程度  

B、r2 表示因变量y的总变异中受自变量x影响的部分所占的比重  

  C、r表示两变量的相关程度   

D、r2 表示在因变量的总的变化中自变量所引起的效应的比例

  E、1-r2则表示残差变量在因变量的变化中所占的份额

11.              在相关分析与回归分析中：

A、据同一资料，相关系数只能计算一个

B、据同一资料，相关系数可以计算两个

C、据同一资料，回归方程只能配合一个

D、据同一资料，回归方程随自变量与因变量的确定不同，可能配合两个

E、回归方程和相关系数均与自变量和因变量的确定无关

12.              下列说法中正确的有：

A．具有明显因果关系的两变量不一定是线性相关关系

B．相关关系的符号可说明两变量相互关系的方向

C．样本相关系数和总体相关系数之间存在着抽样误差

D．具有线性相关关系的变量一定存在因果关系

E、相关系数越大，则回归系数也越大

13.              对于回归系b，下列说法正确的有：

A、b是回归直线的斜率    

B、b的绝对值介于0～1之间

  C、b接近于零表明自变量对因变量影响不大

  D、b与相关系数r 能够相互推导

14.              如果变量x与y之间存在着正线性相关关系，则下列回归方程中肯定错误的有：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A．= 85 – 0.6x     B．= －100+10x     C．=－25－3x

D．= 260 + 1.5x    E．= －80 + 2.5x

15.              直线回归分析中：

A. 根据回归系数可判定相关的方向

B. 两个变量不是对等的关系

C. 利用一个回归方程，两个变量可以互相推算

D. 对于没有明显因果关系的两个线性相关变量可求得两个回归方程

E. 对于有因果关系的两个线性相关变量可求得两个回归方程

16.              直线回归方程=a+bx 中的b 称为回归系数,回归系数的作用是:

A．可确定两变量之间因果关系

B. 可确定两变量的相关方向

C. 可确定两变量相关的密切程度

D. 可确定因变量的实际值与估计值的变异程度

E. 可确定当自变量增加一个单位时，因变量的平均增加量

17.              回归方程可用于：

A、根据自变量预测因变量     B、根据给定因变量推算自变量

  C、用于控制自变量           D、用于控制因变量

判断题

1.    在研究两个变量是否利用回归分析进行分析时，可以先为这两个变量作散点图，观测一下这两个变量是否呈现线性关系。 

2.    两个数值变量在做回归分析时，选那个变量做自变量并不会影响分析的结果。 

3.    两个数值变量在做相关分析时，选那个变量做自变量并不会影响分析的结果。 

4.    如果从散点图中可以看出所有的点都在一条直线附近，那么就可以找出一条直线，用它替代所有的散点，这就是直线回归分析的思想。　　

5.    如果样本相关系数很高，则总体相关系数也必定很高。　

6.    在一元线性回归方程中，回归系数表示自变量每变动一个单位时，因变量的变动值。　

7.    如果两变量的相关系数等于0，说明它们之间不存在任何关系。

8.    在影响因变量变化的所有因素中，除了自变量以外把其它的因素统一综合称为残差变量。如果没有残差变量的影响那么散点图中全部的点都要落在回归直线上。　

9.    如果两个变量x、y的数据在回归直线附近很分散，那么这两个变量的相关系数的绝对值接近于1。　

10.              在研究两个变量关系时，回归分析与相关分析应该结合起来。　

11.              在对数据集(xi、yi)与数据集(ti、ki)作相关与回归分析时，若它们的回归直线是相同的，则它们的相关系数也一定相同。　

12.              在对变量x与y作回归与相关分析时，如果回归直线几乎是水平的，即使这两个变量的相关系数很大，研究者对这样的回归直线通常也是不感兴趣的。　

13.              如果散点是很宽松地分布在回归直线附近，那么点与直线的距离远，意味着残差平方和大，所以相关系数也大。　

14.              在由样本信息对总体进行推断时，检验零假设为“自变量与因变量无关”，它等价于检验“回归系数 b=0”。　

15.              在作回归系数的区间估计时，如果置信区间包含了0点，那么我们就可以认为在总体中，自变量与因变量有关系。　　

16.              在由样本信息对总体进行推断时，检验零假设为“自变量与因变量无关”如果由样本数据计算出 p-值小于0.05，就可以认为根据样本数据建立的回归方程成立，p-值越小说明因变量关于自变量的回归方程越显著。　

17.              自变量是虚拟变量（即有两类的分类变量），因变量是数值变量时，可以作相关与直线回归分析。　

18.              自变量是数值变量，因变量是虚拟变量（即有两类的分类变量）时，可以作相关与直线回归分析。　

19.              如果因变量y关于自变量x的回归方程是统计显著的，但x和y之间不能确定是否有因果关系，那么就不能根据自变量去预测因变量y的取值。　

 

 

参考答案

第一节　回归与相关分析　(64)

单选题 

1.A  2.B  3.C  4.C  5.B   6.D   7.C  8.B   9.C   10.A   11.D   12.A  13.B   14.D  15.A   16.C  17.A  18.D  19.B   20.D  21.B   22.C   23.C  24.A   25. C    26.D   27.A  28.B

多选题

1.CE 2.ACD 3.ABE 4.ABCD 5.ABD  6.BD  7.BD

8. BE  9. BCD 10.BCDE 11.AD  12.ABC  13.ACD  14.AC 15. ABD  16.BE  17.AD

判断题

20.                对

21.                错

22.                对

23.              　对

24.              　错

25.              　错

26.                错

27.              　对

28.              　错

29.              　对

30.              　错

31.              　对

32.              　错

33.              　对

34.              　错

35.              　对

36.              　对

37.              　错

38.              　错