、
的值应是下面方程组的解，即： 
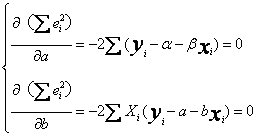
经整理可得求
、
的标准方程组： 
解方程得：
用最小平方法求出的回归方程
对于样本的所有观察值，从整体上看是最理想的拟和，它是假设因变量
只受自变量
影响的函数表达式。 【例8.4】根据表8-2资料，拟和业务考试成绩与每月销售额的样本回归方程：
解：
即：
上式中回归系数为0.2710，表示业务考试成绩每提高1分，每月销售额平均会提高0.2710万元。
四、估计标准误差
(一)估计标准误差的概念。估计标准误差是用来说明回归方程代表性大小的统计分析指标。可简称为估计标准差或估计标准误，起计算原理与标准差基本相同。估计标准误差说明理论值(回归线)的代表性。若估计标准误差小，表明回归方程准确性高，代表性大；反之，估计不够正确，代表性小。
(二)估计标准误差的计算方法
1.根据定义公式计算。估计标准误差，是指因变量实际值与理论值离差的平均数。其定义公式为：
式中，
表示估计标准误差；
表示数据的项数。 2.根据回归直线方程中的参数
、
计算。其计算公式为： (1)资料未分组：
(2)资料已分组：
(三)估计标准误差与相关系数的关系。这两个指标在数量上具有如下关系：
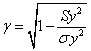
式中，r表示相关系数；
表示因变量数列的标准差；
表示估计标准误差。 在实际应用中，一般不常用这种方法计算相关系数，因为这种计算方法存在两个问题：
(1)需要先求出回归直线方程，计算出估计标准误差，才能求出相关系数。而从一般的认识程序来看，只有相关关系密切的情况下，计算回归方程才有意义；如果关系不密切，下一步的计算就不必要了，因而要求先计算相关系数以判断相关关系的密切程度。
(2)这种计算方法得出的r，难以判断是正相关还是负相关。
从估计标准误差与相关系数相联系的两个公式中可以看出，相关系数和估计标准误差的变化方向是相反的。当相关系数越大时，估计标准误差越小，这时，相关密切程度较高，回归直线的代表性较大；当相关系数越小时，估计标准误差越大，这时相关密切程度较低，回归直线的代表性较小。