实验一 氢、氘原子光谱
18世纪中叶有人已发现炽热气体的火焰发出的光谱是线状光谱是线状光谱，随后发现各种元素的受激原子发出的发射光谱或白光被原子气吸收时产生的吸收光谱也都是线状光谱。到了19世纪末，分辩本领较大的衍射光栅出现以后，基尔霍夫首先指出一定元素的原子只能发射或吸收一些该元素特定频率的谱线。一定元素的原子光谱线的排列具有明显的规律性，它反映了原子及其电子壳层结构的特性。因此研究原子光谱的规律是了解原子结构的重要手段之一。
氢原子光谱是在所有原子光谱中最简单、最基本的光谱。它有5个相互独立的光谱线系，即赖曼（Lyman）系、巴尔末（Balmer）系、帕邢（Paschen）系、布拉开（Blackett）和普丰特每个线系中，各条谱线的强度和相邻谱线的间隔都向短波长方向有规律地递减。
在氢、氘原子光谱实验中，可以观察到由同位素效应引起的氢、氘原子光谱的巴尔末系前6条氢谱线的波长，并采用适当的辅助手段和个别常量，就能测得与公认值符合得很好的许多基本物理；如氢的巴尔末系的线系限，氢的里德伯常数，电离电势和电子的荷质比e/m等等，本实验还为我们提供了一些微观量的测定方法。
拍摄氢、氘原子光谱可以使用平面光栅摄谱仪，它是光谱实验常用仪器之一。应在了解其基本结构、工作原理的基础上，学会正确的使用方法。
【预习提要】
氢原子光谱是最简单的原子光谱，用中等色散率的摄谱仅拍摄的底片上谱线的排列具有明显的规律性。氘是氢的同位素，由于两者原子核质量的差异在光谱上导致它们的巴尔末系的相应各条谱线产生位移——同位素效应。本实验根据同位素效应验证氘核质量2倍于氢核质量，从中了解原子光谱，反映原子结构和运动的特性。为此应了解下列问题：
1．氢原子光谱含有相互独立的5个光谱线系，它们的名称是什么？其中哪个线系位于可见光区？
2．光谱同位素效应与氢、氘原子里德伯常数的差异之间有什么联系？
3．制定一个用WPC-100型
【实验原理】
1．巴尔末公式与里德伯常数
氢原子光谱的巴尔末线系的可见光波段有条比较明亮的谱线，如图（1-1）所示。
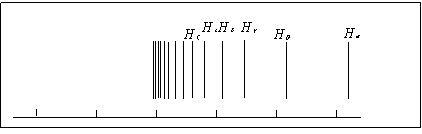
图1-1
表1-1
|
谱线名称 |
量子数 |
颜色 |
波长（单位：nm） |
|
Hα |
3 |
红 |
656.279 |
|
Hβ |
4 |
深绿 |
486.133 |
|
Hγ |
5 |
青 |
434.047 |
|
Hδ |
6 |
紫 |
410.147 |
|
Hε |
7 |
紫 |
397.007 |
|
Hζ |
8 |
紫 |
388.905 |
氢原子光谱谱线的规律性，促使人们去寻找一个表示这些谱线波长的以验公式。1885年巴尔末提出经验公式，表示这些谱线的波长大小：
式是
正整数。364.56为基本数，1896年里德伯(Rydberg)引用波长的倒数——波数
，将巴尔末经验公式改写成光谱项概念的形式：
(1.1)
式中R为里德伯常数。此式完全是从实验中得到的经验公式，然而它在实验误差范围内与测定值的符合是非常惊人的。在这些经验公式的基础上，玻尔（Bohr）利用普朗克（Planck）的量子假设和经典物理理论建立了氢原子理论。根据玻尔理论，原子的能量是量子化的，即原子具有能级。每条光谱线的产生，都是处于相同状态的原子中的电子从一个能级跃迁到另一个较低的能级时释放出能量的结果。将玻尔关于氢原子理论推广到视原子核的质量与电子质量相比为有限且原子核与电子都绕它们的质心转动的情况时，可用下式表示氢原子光谱各线系每条谱线的波数：
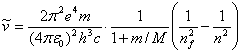(1.2)
式中
为电子电荷，
为普朗克常数，
为光速，
为电子质量，
为氢原子核的质量，
为真空中的介电常数。（1.2）式中的
对于已知一线系取一定的整数，而
，
，
，……等为取值从比大1的整数开始的一系列整数。当=2时，（1.2）式变为巴尔末公式。将（
(1.3)
其中
代表将原子核的质量与电子质量相比视为无穷大（即假定核固定不动）时的里德伯常数。
2．同位素效应与
由（1.3）式可见R是随M变化的。对不同元至少或同一元素的不同同位素，M的值不等，故R亦不同。如果氢原子同位素存在，并且用符号
来表示，则
的巴尔末系各条谱线的波数与
的巴尔末系的相应谱线的波数应是有区别的。反映在谱线上，就应该是核质量大的
的谱线相对的谱线向波数增大的方向发生位移，称为同位素效应。但是又从（1.3）式可以看出，由于
，所以对于
的影响很小，和的相应谱线的波数相差不大，因此大光谱上形成的将是很难分开的双线或多重线。
1932年尤莱（H. C. Urey）、布里克威得（F. G. Brickwedde）将氢放电管中的重氢的浓度提高到正常值以上以便增强通常难以检测的氘谱线的强度，然后激发摄谱，发现氢的巴尔末系各条谱线都是双线，这是氢有两种同位素存在的重要实验证据，若能算出两者的核质量比，则可判定这两种同位素就是氢
和氘
或
。
根据巴尔末公式
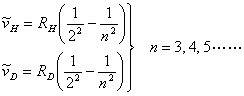
和
分别为氢和氘谱线的波数。
通过对摄得的H和D的巴尔末系各条谱线所测得的波数值及与之间相应的
值一起代入上式后可以求出各自的里德伯常数。将氢（H）和氘（D）的里德伯常数按（
（1.4）
(1.5)
式中
分别为H和D原子核的质量。将（1.4）式除以（1.5）式得
