实验二 塞曼效应
英国物理学家法拉第(M．Faraday)在1862年做了他最后的一个实验，即研究磁场对光源的影响的实验。当时由于磁场不强，分光仪器的分辨率也不大，所以没有观测到在磁场作用下光源所发出的光的变化。34年后，1896年荷兰物理学家塞曼(P．Zeeman)在莱顿大学重做这个实验，他在电磁铁的磁极间将食盐(NaCl)放入火焰中燃烧发出的钠光，用
当时原子结构的量子理论尚未产生，洛仑兹用经典的电子理论对这一现象进行了理论计算，得出所谓正常塞曼效应的结果，即当光源在外磁场的作用下，一条谱线将分裂成三条(垂直于磁场方向观察)和二条(平行于磁场方向观察)偏振化的分谱线。
当实验条件进一步改善以后，发现多数光谱线并不遵从正常塞曼效应的规律，而具有更为复杂的塞曼分裂。这现象在以后的30年间一直困扰着物理学界，从而被称为反常塞曼效应。1925年乌仑贝克和古兹米特为了解释反常塞曼效应和光谱线的双线结构，提出了电子自旋的假设。应用这一假设能很好地解释反常塞曼效应。也可以说：反常塞曼效应是电子自旋假设的有力根据之一。
普列斯顿(Preston)对塞曼效应实验的结果进行了深入研究，1898年发表了普列斯顿定则。即同一类型的线系，具有相同的塞曼分裂。龙格(Runge)和帕邢(Paschen)也进行了大量的实验研究，1907年发表了龙格定则。即将所有塞曼分裂的图象，都可用正常塞曼效应所分裂的大小(做为一个洛仑兹单位)的有理分数来表示(见附注一)从他归纳钩结果中可以一目了然地看到所有塞曼分裂的图象和规律。
综上所述。反常塞曼效应的研究推动了量子理论的发展和实验手段的进步，近年来在原子吸收光谱分析中用它来扣除背景，以提高分析的精度。在天文工作上，用塞曼效应来测量太阳和星体表面的磁场强度等等。
本实验是用高分辨率的分光仪器(如法布里—珀罗标准具)去观察或拍摄汞的谱线(546.lnm)的塞曼效应，测量它分裂的波长差，并计算出电子的荷质比(e／m)的值。
【预习提要】
塞曼效应是获诺贝尔奖的重要实验，在原子物理学的学习中，已进行了外磁场对原子作用的理论计算，本实验以这一理论为基础，具体做某一条谱线的塞曼效应实验。预习中耍弄清以下几点：
1．什么叫正常塞曼效应?它和反常塞曼效应有何不同?本实验是做汞绿光(546.lnm)的塞曼效应，依据式(2.2)和选择、偏振定则计算其塞曼分裂。
2．法布里—珀罗标准具的相邻光束光程差
，它的分辨率为何比较高，与哪些因素有关?间隔圈的距离
取多少为好?
3．讲义中的(2.6)、(2.7)、(2.8)式各代表什么意义?
4．如何观察塞曼效应的线偏振和圆偏振?
【实验原理】
1． 原子的总磁矩与总角动量的关系
原子的总磁矩由电子磁矩和核磁矩两部分组成，由于核磁矩比电子磁矩小三个数量级以上，所以暂时可只考虑电子的磁矩这一部分。原子中的电子做轨道运动时产生轨道磁矩，做自旋运动产生自旋磁矩。根据量子力学的结果，电子的轨道角动量
和轨道磁矩
以及自旋角动量
和自旋磁矩
在数值上有下列关系：
，=
，
，=
式中e，m分别表示电子电荷和电子质量；L，S分别表示轨道量子数和自旋量子数。轨道角动量和自旋角动量合成原子的总角动量
，轨道磁矩和自旋磁矩合成原子的总磁矩
，如图2-1表示。
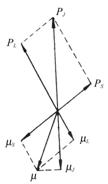
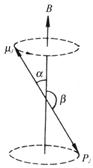
图2-1
由于和
的比值是和
的比值两倍，因此合成的原子总磁矩不在总角动量
的方向上。但由于和是绕旋进的，因此，和都绕的延长线旋进。把分解成两个分量：一个沿的延线，称作
，这是有确定方向的恒量；另一个是垂直于的，它绕着转动，对外平均效果为零。对外发生效果的是。按照图2-1进行矢量运算，可以得到与数值上的关系为：
式中g=1+
叫做朗德因子，它表征单电子的总磁矩与总角动量的关系，而且决定了能级在磁场中分裂的大小。具有两个或两个以上的原子，可以证明磁矩与原子的总角动量的表达式上式相同。但g因子随着藕合类型的不同有两种计算方法。对于LS耦合，与单原子的g因子有相同的形式，只是L,S和J是各电子耦合后的数值。若是Jj耦合，g因子的表达式为：
如果原子有n个电子，
，
分别表示一个电子的J值和g因子。
也可能是(n-1)个电子LS耦合的结果。
2．外磁场对原子能级的影响
设原子某一能级的能量为
，在外磁场（磁场应强度为
）的作用下，原子将获得附加的能量
，则
为磁量子数。
，共有
个值。因此，原来的一个能级将分裂为个子能级。子能级的间隔相等，并正比于和朗德因子
，对于L-S耦合的情况下
（3.1）式中的
为波尔磁子，
。
设频率为
的光谱线是由原子的上能级
跃迁到下能级
而产生（即
），在外磁场的作用下，上下两能级各获得附加能量
、
。因此，每个能级各分裂成
个和
个子能级。这样，上下能级之间的跃迁，将发出频率为
的谱线，并有
分裂后的谱线与原谱线的频率差将为
换以波数表示
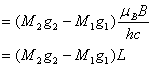（2.2）