假定晶体中某一方向上原子面网之间的距离为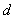 ,X射线以夹角 ,X射线以夹角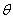 射入晶体,如图17-2所示,从原子面网P1和P2上产生二条衍射线D1、D2,其光程差为AB+BC, 而AB=BC= 射入晶体,如图17-2所示,从原子面网P1和P2上产生二条衍射线D1、D2,其光程差为AB+BC, 而AB=BC=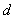 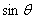 ,故AB+BC=2 ,故AB+BC=2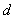 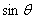 。我们知道,只有当光程差等于入射光波长 。我们知道,只有当光程差等于入射光波长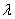 的整数倍 的整数倍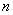 时,也就是 时,也就是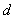 和 和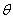 之间应满足布拉格(Bragg)方程,才能产生加强的衍射线。 之间应满足布拉格(Bragg)方程,才能产生加强的衍射线。
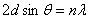 (17—1) (17—1)
图17-2表示与入射的X射线成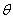 夹角的某一晶面的衍射情况,如将图2中这个晶面以 夹角的某一晶面的衍射情况,如将图2中这个晶面以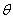 为夹角绕入射的X射线旋转一周,则衍射线形成连续的圆锥体表面,如图17-3所示。这个圆锥以入射线I方向为轴,其半圆锥角等于2 为夹角绕入射的X射线旋转一周,则衍射线形成连续的圆锥体表面,如图17-3所示。这个圆锥以入射线I方向为轴,其半圆锥角等于2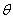 。由于不同方向上原子面网之间的距离具有不同的 。由于不同方向上原子面网之间的距离具有不同的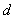 值,因此对应于不同 值,因此对应于不同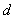 值的原子面网组,只要其夹角( 值的原子面网组,只要其夹角(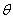 值)能符合(17-1)式的关系,都能产生角锥形的衍射线组,其半圆锥角分别为2 值)能符合(17-1)式的关系,都能产生角锥形的衍射线组,其半圆锥角分别为2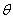 1,2 1,2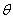 2,2 2,2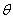 3…,,当晶面与入射X射线之间的夹角 3…,,当晶面与入射X射线之间的夹角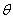 大于45º时,产生背反射衍射(衍射角 大于45º时,产生背反射衍射(衍射角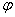 =90º- =90º-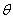 )。 )。

图17—2 原子平面网对X射线的衍射

图17—3 晶面与X射线的夹角为立体角时的衍射情况
[主要数据分析]
在本实验中,不是将具有各种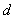 值的被测晶面以 值的被测晶面以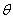 夹角绕入射X射线旋转,而是将被测样品磨成粉末,其线度一般在10-3~10-5mm之间,将这样的样品做成粉末条,则试样中的晶体作完全无规则的排列,存在着各种可能的晶面取向,因而总有许多小晶面处于适合各个衍射条件的位置上,获得如图3那样一组组角锥形衍射图。 夹角绕入射X射线旋转,而是将被测样品磨成粉末,其线度一般在10-3~10-5mm之间,将这样的样品做成粉末条,则试样中的晶体作完全无规则的排列,存在着各种可能的晶面取向,因而总有许多小晶面处于适合各个衍射条件的位置上,获得如图3那样一组组角锥形衍射图。
当一圆筒状照相底片如图17-4(a)那样与入射X射线处于正交的位置时,则各个角锥形衍射线组在底片上曝光形成一对对弧线段,将底片展开为图17-4(b)所示,图17-5为图17-4(b)的平面图,反映了各对弧线之间的距离2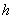 与衍射角2 与衍射角2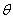 间的关系。 间的关系。
测量底片上各对弧线之间的长度2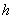 ,可有下式求得 ,可有下式求得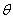 值。 值。
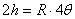 ( (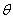 用弧度表示) 用弧度表示)
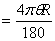 ( (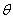 用角度表示) (17—2) 用角度表示) (17—2)
式中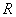 为粉末照相机内感光层片的内圆半径。 为粉末照相机内感光层片的内圆半径。
将(1)式变形为:
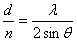 (17—3) (17—3)
把求得的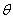 值带入(17-3)式,可得一系列 值带入(17-3)式,可得一系列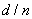 值,这是物相图中最主要的一组衍射数据。 值,这是物相图中最主要的一组衍射数据。
通过上述过程可得到一组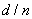 值,根据这组数据去查对标准卡片索引,在误差要求范围内与卡片中数据完全对应,即可得知该被测物质的化学式习惯用名,以及有关的各种晶体学数据。 值,根据这组数据去查对标准卡片索引,在误差要求范围内与卡片中数据完全对应,即可得知该被测物质的化学式习惯用名,以及有关的各种晶体学数据。

图17—4(a)粉末条、底片、入射X射线和衍射线的相对位置

图17—4(b)角锥形衍射图在底片上的曝光情况

图17—5 试样、底片、入射X射线和衍射线相对位置的平面图
|