|
分子的结构可以近似地看成是由电子云和分子骨架(原子核及内层电子)所构成。由于其空间构型不同,其正、负电荷中心可以是重合的,也可以是不重合的,前者称为非极性分子,后者称为极性分子。
(一) 偶极矩的概念和单位
(二) 偶极矩的分类
(三) 极化的概念
(四) 偶极矩和极化的关系
(五) 微观性质和宏观性质的关联
分子的偶极矩和它的宏观性质介电常数、密度、折射率紧密联系,克劳修斯、莫索第和德拜从电磁理论得到了克劳修斯—莫索第—德拜方程:
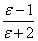 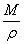 = =  NA NA = = 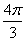 NA(aE + aA + NA(aE + aA +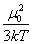 ) (11-8a) ) (11-8a)
其中M是分子量,r是温度为T时的密度,NA是阿佛加德罗常数。利用这个方程,可测定分子的偶极矩与极化率,为此常将式中左端记作P,称为摩尔极化度,即:
P =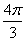 NA (aE + aA + NA (aE + aA +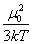 ) (11-8b) ) (11-8b)
此式只适用于气体、极性分子在非极性溶液中的稀溶液或非极性液体。根据溶液的加和性,德拜1929年提出对极性溶质和非极性溶剂所组成的二元体系其摩尔极化度可由下式计算:
P12=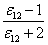 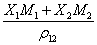 =X1P1 + X2P2 (11-9) =X1P1 + X2P2 (11-9)
式中下标12表示溶液,1表示溶剂,2表示溶质,X1, M1, P1和X2, M2, P2分别代表溶液中溶剂和溶质的摩尔分数,摩尔质量和摩尔极化度,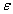 12,r12和P12分别代表溶液的相对介电常数,密度和摩尔极化度。对于稀溶液我们假定非极性溶剂的摩尔极化度P,不随浓度变化,且等于纯态下的摩尔极化度P0,即P1=P0,则上式可改写为: 12,r12和P12分别代表溶液的相对介电常数,密度和摩尔极化度。对于稀溶液我们假定非极性溶剂的摩尔极化度P,不随浓度变化,且等于纯态下的摩尔极化度P0,即P1=P0,则上式可改写为:
P12=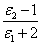 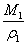 X1 + (PA2 + PE2 + X1 + (PA2 + PE2 +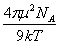 ) X2 (11-10) ) X2 (11-10)
根据光的电磁理论,在同一频率的高频电场作用下,透明物质的介电常数与折光率有如下关系:
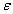 = n2 (11-11) = n2 (11-11)
习惯上用摩尔折射率R12来表示高频区测得的极化度, 在高频区原子极化和定向极化都很小可忽略,仅剩下电子极化,所以按照上述方法也可以推得P12的。
R12 =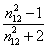 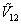 = = 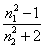  X1+ PE2X2 (11-12) X1+ PE2X2 (11-12)
忽略PA2这一项, 用方程(11-10)-(11-12)即得:
P12-R12=( - -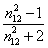 ) )
=(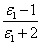 - -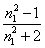 ) )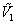 X1+ X1+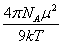 X2 (11-13) X2 (11-13)
在稀溶液中我们假定物质的偏摩尔体积与摩尔体积相等,且对于稀溶液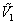 X1>> X1>>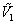 X2,在一定温度下,令: X2,在一定温度下,令:
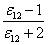 - -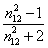 = Y (11-14) = Y (11-14)
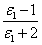 - -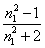 = A (11-15) = A (11-15)
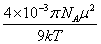 = B (11-16) = B (11-16)
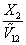 = =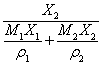 = C2× 10-3 (11-17) = C2× 10-3 (11-17)
则(11-13)式就变为:
Y = A + BC2 (11-18)
因此,在实验中,只要我们测定出各种不同浓度溶液的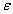 12,n12,算出Y和C2,用Y对C2作图,便可得到一直线,其斜率为B,因此μ就可用下式求得: 12,n12,算出Y和C2,用Y对C2作图,便可得到一直线,其斜率为B,因此μ就可用下式求得:
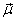 = =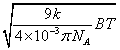 = = 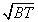 0.405(Debye) (11-19) 0.405(Debye) (11-19)
┆返回 实验原理┆
|