★   阿基米德分牛问题 Archimedes' Problema Bovinum 

太阳神有一牛群，由白、黑、花、棕四种颜色的公、母牛组成 .   在公牛中，白牛数多于棕牛数，多出之数相当于黑牛数的 1/2+1/3 ；黑牛数多于棕牛数，多出之数相当于花牛数的 1/4+1/5 ；花牛数多于棕牛数，多出之数相当于白牛数的 1/6+1/7. 在母牛中，白牛数是全体黑牛数的 1/3+1/4 ；黑牛数是全体花牛数 1/4+1/5 ；花牛数是全体棕牛数的 1/5+1/6 ；棕牛数是全体白牛数的 1/6+1/7.

问这牛群是怎样组成的？  

★ 德 · 梅齐里亚克的法码问题

The Weight Problem of Bachet de Meziriac  

一位商人有一个 40 磅 的砝码，由于跌落在地而碎成 4 块 . 后来，称得每块碎片的重量都是整磅数，而且可以用这 4 块来称从 1 至 40 磅之间的任意整数磅的重物 .

问这 4 块砝码碎片各重多少？

★ 鲁卡斯的配偶夫妇问题 Lucas' Problem of the Married Couples

 n 对夫妇围圆桌而坐，其座次是两个妇人之间坐一个男人，而没有一个男人和自己的妻子并坐，问有多少种坐法？

★ 费马 - 欧拉素数定理 The Fermat-Euler Prime Number Theorem 

每个可表示为 4n+1 形式的素数，只能用一种两数平方和的形式来表示 .

★   德里安倍立方问题 The Deliaii Cube-doubling Problem 

画出体积为一已知立方体两倍的立方体的一边 .

★ 正十七边形 The Regular Heptadecagon 

画一正十七边形 .

★ 斯坦纳的圆问题 Steiner's Circle Problem

在所有等周的（即有相等周长的）平面图形中，圆有最大的面积 .   反之：在有相等面积的所有平面图形中，圆有最小的周长 .

★ 斯坦纳的球问题 Steiner's Sphere Problem 

在表面积相等的所有立体中，球具有最大体积 .

在体积相等的所有立体中，球具有最小的表面 .

★ 能够培养几何直觉的若干趣题：

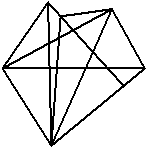
1 、串通一气

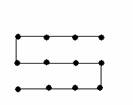
上图中的 12 个点被 5 条线段串连了起来，而且这些线段是连着一笔画成的。

你可以做得更好：同样是把这 12 个点串连起来，要求：

（ 1 ）连着一笔画；

（ 2 ）用 5 条线段；

（ 3 ）结束在开始的那点，从而形成一个闭合的回路；

（ 4 ）每个点只能经过一次（但线段可以相互交叉）

2 、 大小正方形

小正方形的边长为 1 米 ，大正方形的边长为 1.5 米 。大正方形的一个顶点正好位于小正方形的中心。

大正方形的边长与小正方形的两条边相交，把它们都分为三分之一和三分之二的两个部分。

这两个正方形的重叠部分面积是多少？

3 、点与线

你可以把 3 个点连成 3 条直线，每条直线上有 2 个点。你能不能把 10 个点摆放得可以连成 5 条直线，每条直线上有 4 个点？

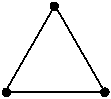
4 、矩形中的矩形

这幅图中一共有多少个矩形？（ 注：正方形也是矩形 。）

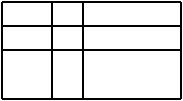
5 、矩形中的四边形

这幅图中一共有多少个四边形？

6 、两枚硬币

有两枚一模一样的硬币，其中一枚保持不动，而另一枚围着它转动，转动时始终靠着且没有滑动。

当第二枚硬币围绕着第一枚硬币转完一圈的时候，它自转了几圈？

（ 不能用实际的硬币来解题 ！）

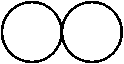
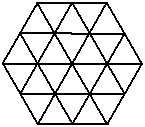
7 、六边形中的三角形

这幅图中一共有多少个三角形？

8 、马到成功

国际象棋中的马最多可以威胁到 8 个格子。

你必须在 8 × 8 的棋盘上放多少个马，才能使每个格子，要么被一个马所占据，要么受到至少一个马的威胁？

9 、平均分隔

你应该在这正方形内部的什么地方放上奇数根木棒，从而把这正方形隔成面积相等的四个区域？

10 、三角形知多少？

这幅图中一共有多少个三角形？

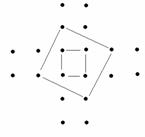
11 、删点破方

下图中有 20 个点，顶点为其中 4 个点的正方形有许多个。这里只画出了两个。

你必须在其中删掉多少个点，才能使所剩下的点中的任何 4 个点都不能形成一个正方形？

12 、四位王后

你能不能把 4 个后放在这棋盘上，使得任何一个后都不能“吃”其他的后。

（ 国际象棋中的后可以沿水平、竖直或对角的方向走过任意多个格子。 ）

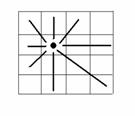
13 、图形重组

在这幅图中， 8 条相等的线段（ 4 条水平， 4 条竖直）形成了 14 个正方形：

1 × 1 的正方形 9 个

2 × 2 的正方形 4 个

3 × 3 的正方形 1 个

你能不能把这 8 条线段重新组成一个图形，使得其中有

2 个正方形

24 个等腰三角形？

正方形的大小是不相同的。由 4 个大三角形， 8 个中等大小的三角形， 12 个小三角形。

14 、五边形中的三角形

这幅图中一共有多少个三角形？你能不能有计划有步骤地数出这些三角形，一个都不漏下？

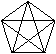
15 、五角星中的四边形

这幅图中一共有多少个四边形？这里四边形指的是任何有 4 条边的图形。（ 注意：有 10 个以上。 ）

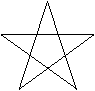
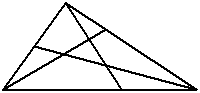
16 、斜三角形中的三角形

这幅图中一共有多少个三角形？