榆林学院学报 第 15 卷 第 5 期 2005 年 11 月
新课程理念下的数学观与数学教学观
宋文檀
摘 要 : 数学本质是一个认识论的问题。如何认识数学与数学教学的本质 , 形成与当今数学教学改革相适应的数学观与数学教学观 , 这是新的课程改革所面临的一个重要课题。
关键词 : 数学课程改革 ; 数学本质 ; 数学观 ; 数学教学观
1 问题的提出
数学观是人们对数学总的认识和看法。数学教学观是数学教师关于数学教学的本质以及学生数学学习过程的一种认识。可见 , 回答“数学是什么”、“数学教学是什么”的问题 , 实际上是反映教师数学观和数学教学观的根本问题。作为一名数学教师 , 影响其从事数学教育教学最重要的因素是数学教育观念 , 即数学观和数学教学观。面对当今已经物化了的数学课程改革 , 数学教师应如何认识数学与数学教学的本质 , 形成怎样的数学观与数学教学观才能逐步适应教育改革对数学教师素质的要求是我们应该深入研究的一个重要问题。
2 数学本质与数学观
2.1 数学本质认识概述
数学作为对客观世界的一种认识 , 尽管人类认识数学本质经历了漫长的历程 , 但始终遵循着实践—认识—再实践的认识规律。从认识论看 , 对数学本质的认识 , 长期以来存在着数学是“经验科学”、数学是“演绎科学”或者是“经验科学与演绎科学的辩证统一”的不同认识。历代数学家、数学哲学家对数学本质的认识从来没有一个统一的结论 , 但他们各自从不同的视角揭示了数学的内在规律 , 推动了数学的不断向前发展。正如美国著名数学家可朗 (R · Courant) 在《数学是什么》一书中指出 : “数学作为人类智慧的一种表达形式 , 反映生动活泼的意念 , 深入细致的思考 , 以及完美和谐的愿望 , 它的基础是逻辑和直觉 , 分析和推理 , 共性和个性 , 虽然 , 不同的传统学派各自强调不同的侧面 , 但是只有双方对立的力量相互依存和相互斗争 , 才真正形成数学科学的生命力、可用性以及至上的价值。” [1] 一方面 , 数学以严谨的演绎思维、逻辑推理充分发挥了对人的“心智训练”的功能 ; 另一方面 , 由数学的经验性和实践性衍生来的数学应用的广泛性 , 直接决定了数学的应用价值。
2.2 数学观的结构与分类
2.2.1 数学观的结构
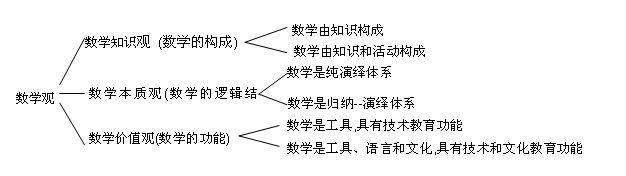
数学观是人们对数学本质的理性思考 , 它属于数学哲学范畴。在本体论方面 , 涉及数学研究对象问题、数学对象的存在性和客观性问题。在认识论方面 , 涉及数学的真理性问题 , 数学真理客观性问题 , 数学发展的动力和源泉问题。数学观主要包括数学知识观、数学本质观和数学价值观三个方面 , 而每一方面较突出地存在着两种不同的认识 , 可综合表述如下 :
2.2.2 数学观的分类
对数学本质的不同认识反映出不同的数学观 , 美国学者 Emest 把数学观分为三类 [2] : a. 动态的易谬主义数学观 , 把数学看作一种处于探索发展过程中的知识 , 它一定包含有错误、尝试改正与改进的过程。 b. 静态的绝对主义的数学观 , 把数学看成是一种静态的永恒不变的科学 , 认为数学是一个精心组织起来的高度统一且十分严谨的逻辑体系。 C. 工具主义的数学观 , 把数学看作由一系列概念、公式、法则、定理、推理等构成的真理集合 , 数学教学就是在解决问题中如何运用这些真理。
由于数学产生和发展的历史悠久 , 加之数学与各种哲学观念复杂的历史渊源 , 数学观——从两千三百多年前的毕达哥拉斯学派的神秘主义数学观 , 到古典柏拉图主义的“数学理念世界”数学观、到现代柏拉图主义的“先验论”数学观 , 到近代数学基础三大学派的逻辑主义、形式主义、直觉主义所形成的数学观 , 再到现代绝对主义数学观、可误主义数学观、社会建构主义数学观——一直体现着人们对数学本质认识的时代特征。可以看出 , 人类对数学本质漫长的认识历程正是数学观的不断演进过程。
3 新课改理念下的数学教学观
3.1 数学观深刻影响着数学教学观
既然存在着不同的数学观 , 那么每个数学工作者总是自觉或不自觉地接受着某种数学观。例如 , 在数学本质观上 , “从事教学工作的人 , 如果认为数学是一门演绎科学 , 那么他就不会关心实践提出的数学问题 , 而专注数学的逻辑问题 ; 反之 , 如果认为数学是一门经验科学 , 他就不会去关注数学的逻辑问题 , 而关心实践提出的问题 ; 如果认为数学是一门经验性与演绎性辨证统一的科学 , 他就会既关心实践提出的数学问题又关心数学的逻辑问题。” [3] 对数学教师来说 , 数学观直接影响着数学教学观 , 教师对数学知识本质的认识和理解直接决定着他对数学知识传授方式的选择。如果教师认为数学是“计算 + 推理”的科学 , 那么他在教学中就会严守数学知识本身的逻辑体系 , 注重数学知识的传授 , 强调运算能力、逻辑思维能力和空间想象能力的培养 , 而不关心数学知识的学习过程和应用问题。又如 , 《新课程标准》对数学本质采用了描述性定义 , 指出“数学是人们生活、劳动和学习不必可少的工具” , “数学是一种技术” , “数学是人类用于交流的语言” , “数学是一种文化” , “数学能赋予人创造性” , “数学是人类的一项活动” [4] 等等。《新课程标准》这种动态的数学本质观一方面为深刻认识数学的本质提供了新的视角 , 它是对传统数学观的一种超越 ; 另一方面 , 这些观点从不同的侧面反映了不同的数学观。如果教师把数学理解为一种工具 , 那么他就强调数学的应用性 , 关心数学与其它学科及社会之间的联系 ; 如果教师把数学视为一种语言 , 那么他就会注重师生、学生之间的平等沟通和对话 ; 如果认为数学能赋予人们创造性 , 那么他就把数学知识的发生、发展演进过程作为学生发现探索、进行再创造的过程 ; 如果认为数学是人类的一项活动 , 那么他就会注重数学和现实生活的联系 , 即用数学的思想和方法不断地把与实际问题有关的材料整理和组织到数学教学中。 [5] 由此可见 , 对数学本质的不同认识 , 体现出不同数学教学思想 , 或者说 , 有什么样的数学观 , 就有什么样的数学教学观。
3.2 数学教师数学观与数学教学观的转变
当前正在我国进行的数学教育的重大改革 , 体现了“以人为本 , 以学生发展为本”的基本理念。提倡数学教育要紧密联系学生的生活实践 , 要从学生现有的认知结构出发进行教学 , 强调问题解决 , 强调主体活动 , 要让学生通过活动来建构对数学意义的理解、通过解决数学问题提高应用数学知识的能力。数学教学要满足学生个人兴趣爱好 , 要根据学生的个性特点进行教学。这实际上反映了数学教育改革的一种世界潮流。面对教育改革大潮 , 教师的教育教学观念相应地也应有大的改变。
3.2.1 数学观的转变
我们认为 , 现在多数数学教师所持有一种“科学主义 + 绝对主义 + 工具主义”的数学观。持有这种数学观的教师在教学中明显地体现出 : a. 数学知识是无可置疑的真理 , 教师是知识的拥有者 ; b. 教学过程是授予—吸收的过程 , 学生的学习过程是模仿 + 训练 ; c. 注重知识的传授 , 突出教师的讲解和示范作用。应该看到 , 在长期教学实践中逐步形成的这种数学观 , 有其结构的合理性和必要性。但面对 21 世纪的教育改革 , 数学教学要充分体现“生活化”、“活动化”、“个性化”特征 , 要求数学教师必须更新数学观念 , 深入认识数学本质和历史演进过程 , 不仅有科学的数学观 , 还应从数学哲学层面形成数学文化观念、数学价值观念和数学应用观念 , “逐步从静态的、形而上学的、绝对主义数学观转向到动态的、辩证的、建构的、人文主义和科学主义相结合的数学观。” [6]
3.2.2 数学教学观念的转变
这涉及数学教学观、数学学习观、数学评价观定位问题。教学观念应实现以下几个转变。
3.2.2.1 由传统的教师主导下的教学转变为教师指导下的教学。认识学生的学习过程是学生自己主动建构过程。
3.2.2.2 教师由知识的传授者转变为学生学习活动的设计者、引导者、合作者 , 学生由被动的听课者转变为数学课程知识的探索者、创造者、学习者。体现“数学教学是数学活动的教学 , 是师生之间、学生之间交往互动与共同发展的过程”的教学新理念。
3.2.2.3 数学教学评价由单纯的学习结果评价转向既关注学习结果 , 又关注学生知识、能力、情感、态度及学生学习过程的评价 , 即采用过程评价和结果评价相结合的评价体系。
4 结语
数学观能够从哲学的高度指导数学教育实践 , 它是整个数学教学工作的认识基础。数学教师要用新的教育理念 , 从数学教育哲学的层面认真思考和诠释“数学是什么”、“数学教学是什么”、“数学学习的意义是什么”、“数学教师的角色是什么”、“评价一个好学生的标准是什么”等问题。这些问题实际上是教师数学本质观、数学观、数学教学观的集中体现 , 也是每一个数学教师过去、现在、以至将来做好本职工作必须思考的重大课题。
参考文献 :
[1] 可朗 R. 罗宾 M. 数学是什么 [M ]. 长沙 : 湖南教育出版社 , 1985.
[2] 骆洪才 , 等 . 数学观的层面分析 [J ]. 数学教育学报 , 2004, 13 (3) : 27.
[3] 林夏水 . 数学本质认识论数学观 [J ] . 数学教育学报 , 2002, 11 (3) : 27.
[4] 中华人民共和国教育部 . 全日制义务教育数学课程标准 ( 实验 ) [S ]. 北京 : 北京师范大学出版社 , 2001.
[5] 杨建辉 . 新课程标准下教师教学设计中应具备的几种意识 [J ]. 数学通报 , 2004 (2) : 2- 3.
[6] 黄秦安 . 数学教师的数学观和数学教育观 [J ]. 数学教育学报 , 2004, 13 (4) 24- 26.