归结反演的控制策略
1、宽度优先策略
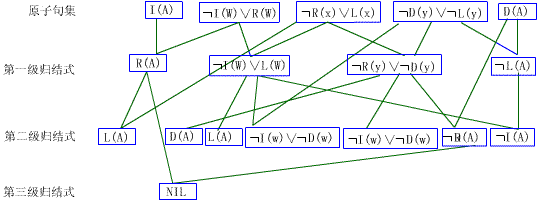
宽度优先策略首先从基本集合生成所有的归结式,再从基本集合和第一级归结式生成第二级归结式,以此类推。显然,宽度优先策略是完备的,但是低效的。下图(图4-2)为上例通过宽度优先策略生成的引导图,注意图中在第三级归结是就产生了空子句,而在上例图4-1中空子句是在第四级才产生的。

图4—2
2、支持集策略
支持集策略是指对每个归结式,其母式子至少有一个是目标公式的否定及其后代(即支持集)。可以证明,只要存在矛盾,支持集反演就存在,即支持集策略是完备的。支持集策略相当于在宽度优先策略中引入了约束条件,因此效率比宽度优先搜索要高。在反演过程中,每个目标公式的否定的后代都可看成一个子目标,由于归结的子句始终包括子目标,并产生新的子目标,因此支持集策略可看成是某种形式的逆向推理。
图4-3为上例通过支持集策略产生的导引图。与宽度优先策略相比,每级产生的归结式减少了,但增加了空子句的深度,一般说来,支持集策略能够减慢每级子句的增长速度。
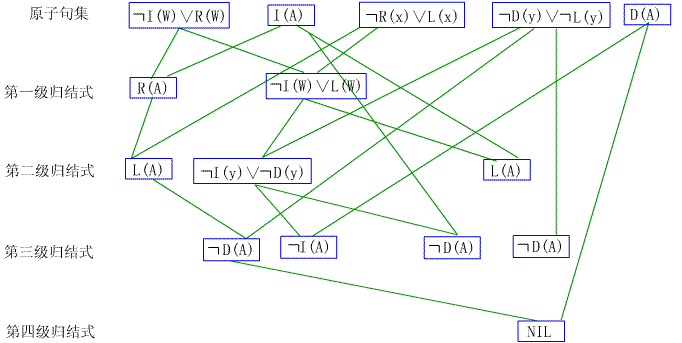
图4—3
3、单元优先策略
单元优先策略是支持集策略的一个改进。不是全部生成每一级所有的归结式,而是优先选取单文字的子句(称作单元)作为一个母体子句。这样,所得到的归结式的文字数目必然比其另外的一个母体子句少。这有利于使归结式朝着空子句的方向生成,因此提高了效率。图4-1的反演树就是由单元优先策略产生的。
4、线性输入形策略
线性输入形策略对每个归结式的要求是,其母体子句至少有一个属于基本集。使用线性输入形策略,仅第一级归结式与宽度优先策略相同,其余各级归结式都减少了数目,因此效率较高。但该策略不是一个完备的策略,例如对下面的子句集:
S={Q(u)Ú P(A), ØQ(w)ÚP(w), ØQ(x)ÚØ P(x), Q(y)ÚØP(y)}
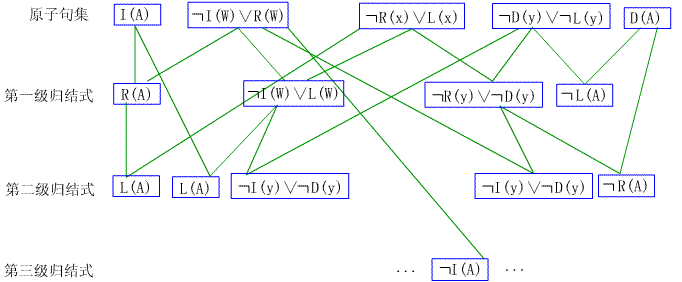
图4—4
集合S是不可满足的,但用线性输入形策略不能产生空子句。图5-4为上例通过线性输入形策略生成的导引图。
5、祖先过滤形策略
祖先过滤形策略对每个归结式规定,其母体子集至少有一个在基本集中,或者是另一个母体子式的祖先。可见祖先过渡性策略类似于线性输入形策略,但要求较宽。这种策略虽然生成的子句比线性输入形策略多,但可以证明该策略是完备的。图4-5是该策略产生的一棵反演树,图中标有*的子句当作一个祖先使用。
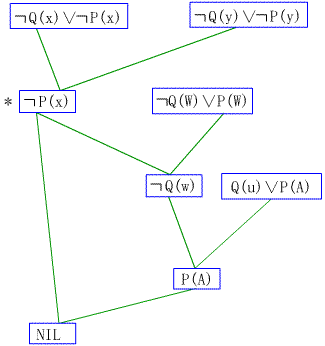
图4—5
在实际应用中,以上策略可以组合起来使用,以提高搜索效率。
习题
设公理集为
("u)LAST(cons(u,NIL),u)
("x)("y)("z)[LAST(y,z)®LAST(cons(x,y),z)]
其中cons是表构造函数,LAST(x,y)表示y是表x的最后一个元素。
(1) 用归结反演法证明如下定理:
($v)LAST(cons(2,cons(1,NIL)),v)
(2)用解答提取过程求表(2,1)的最后一个元素。
(3)简要描述如何使用这个方法求长表的最后一个元素。