提取解答的基本过程
我们通过几个例子说明提取解答的过程。
例1 已知事实如下:
(1)Fido goes where John goes (John走到哪里Fido跟到哪里)。
("x)[AT(JOHN,x)®AT(FIDO,x)]
(2)John is at school (John在学校)。
AT(JOHN,ScHOOL)
解答问题:
(3) where is Fido(Fido在哪里)?
($x)AT(FIDO,x)
首先应证明第三句在逻辑上遵从前两句,然后再找一个x的例,这样就可以解答上述问题了。使用归结反演方法,将上述两个事实公式转换为子句集合为:
{ØAT(JOHN,x)AT(FIDO,x),AT(JOHN,ScHOOL)}
目标公式的否定为 ("x)[ØAT(FIDO,x)]
否定公式的子句形式为 ØAT(FIDO,y)
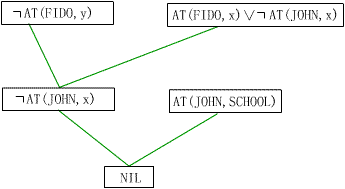
问题的反演树如图1。提取解答的步骤如下:

图1
(1)在目标公式的否定的子句形式中,附加上该子句的否定,得到
ØAT(FIDO,y)ÚAT(FIDO,y)
这种含有一个文字及其否定的子句称为同语反复,或重言式。
(2)进行与上述反演树相同的归结求解,如图2所示,我们将该图称为修改的证明树。
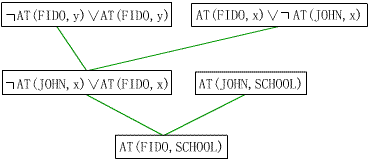
图2
(3)将根结点的子句作为解答子句。
在本例中,图中根结点的子句 AT(FIDO,ScHOOL)就是问题的解答。从归结的观点看,归结式逻辑上遵从事实子句和重言式,而重言式总为真,因此归结式逻辑上遵从事实子句。
例2 已知事实如下:
(1)对所有的x和y,如果x是y的父辈而y是z的父辈,则x是z的祖辈。
("x)("y)("z){[P(x,y)ÙP(y,z)]®G(x,z)}
(2)每个人都有父辈。
("x)($y)P(x,y)
解答问题:
(3)是否存在具体的x和y,使得x是y的祖辈?
($x)($y)G(x,y)
用归结反演法可给出这个问题的证明,其反演树如图3。为了生成修改证明树的方便,在生成反演树时,对被合一的文字作了标记,并将被合一的文字的集合称为合一集。
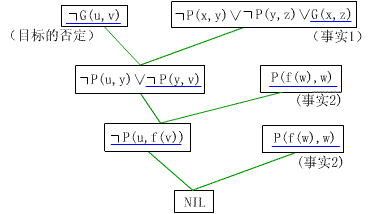
图3
事实2的子句P(f(w),w)包括一个Skolem函数f,建立起一个人与其父辈的映射。修改证明树如图4所示,在修改证明树中使用的合一集与图3所示的反演数中的合一集相同。修改树中根结点的子句G(f(f(v)),v)就是问题的解答。
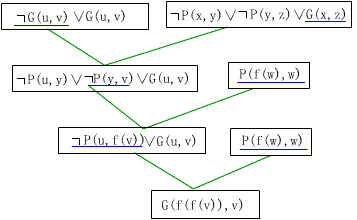
图4
习题
设公理集为
("u)LAST(cons(u,NIL),u)
("x)("y)("z)[LAST(y,z)®LAST(cons(x,y),z)]
其中cons是表构造函数,LAST(x,y)表示y是表x的最后一个元素。
(1) 用归结反演法证明如下定理:
($v)LAST(cons(2,cons(1,NIL)),v)
(2)用解答提取过程求表(2,1)的最后一个元素。
(3)简要描述如何使用这个方法求长表的最后一个元素。