目标公式含有全称量词的情况
当目标公式含有全称量此量化的变量时,目标公式的否定式中会出现Skolem函数,结果会与要求不符。这一点从下面的例子可以看出。
例1 已知事实为
(1)对所有的x,x是p(x)的孩子。
("x)c(x,p(x))
(2)对所有的x、y,如果x是y的孩子,则y是x的父辈。
("x)("y)[c(x,y)®P(y,x)]
解答问题:
(3)对任何一个x,谁是x的父辈?
("x)($y)P(y,x)
目标公式的否定式为
($x)("y)[ØP(y,x)]
目标公式否定式的子句形式为
ØP(y,A)
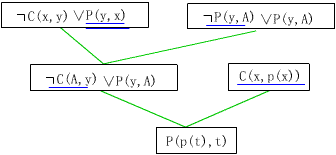
其中A为没有自变量的Skelom函数(即常量)。此例的修改证明树如图442-1所示。解答语句为P(p(A),A)。解答过程中出现的常量A与问题中的“任何一个x”不符。事实上可以证明,在解答提取过程中,可以用新变量代替来自目标公式否定式的子句中的Skolem函数,这些新变量经过替换过程仍会出现在解答语句中。在本例中,经过用新变量代替后的修改证明树如图442-2所示,最后的解答为P(p(t),t)。

图442-1 例1的修改证明树
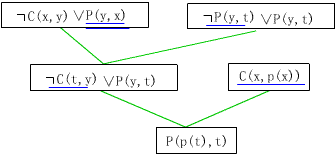
图442-2 例1中变量替换后的修改证明树
例4 给出子句:
P(z,u,z)P(A,u,u)
目标公式为
($x)("z)($y)P(x,z,y)
目标公式否定式的子句形式为
ØP(x,g(x),y)
反演树和修改证明树如图442-3所示,其中Skolem函数g(x)用变量w代替,得到的解答子句为
P(z,w,z)ÚP(A,w,w)
除了变量名外,这个解答与给出的子句是完全相同的。
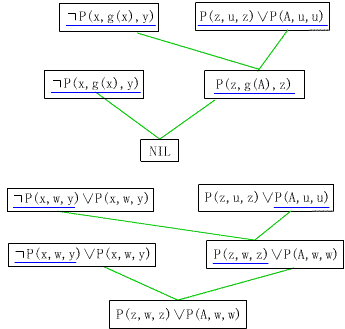
图442-3 例4的反演树和修改证明树
习题
一个积木世界的状态由下列公式集描述:
ONTAbLE(A) cLEar(E)
ONTAbLE(c) cLEar(D)
ON(D,c) HEAVY(D)
ON(b,A) WOODEN(b)
HEAVY(b) ON(N,E)
给出这些公式所描述的状态草图。
下面语句提供了有关描述这个积木世界的一般知识:
每个在任一积木块之上的大的蓝色积木块是在一个绿色积木块之上。
每个重的木制积木块是大的。
所有顶上没有东西的积木都是蓝色的。
所有木制积木块都是蓝色的。
以单文字后项的蕴含式的集合表示这些语句。给出能求解“哪个积木块是在绿色积木块上”这个问题的一致解图。