利用规则转换与或图
正向演绎系统应用规则作用于表示事实的与或图,改变与或图的结构,从而生成新的事实。为应用方便起见,规定规则的形式为
L®W
其中
(1)L是单文字,W式任意的与或表达式。
(2)L和W中的所有变量都是全称量词量化的,默认的全称量词作用于整个蕴含式。
(3)各条规则中的变量个不相同,而且规则中的变量与事实表达式中的变量也不相同。
对规则左侧作单文字的限制虽然会大大简化规则的应用过程,但也限制了规则的应用范围。但是在应用中可以对规则作一些变换,使之满足这一要求。例如对(L1∨L2)®W 形式的规则,可以转换成两条等价的规则L1®W和L2®W。
例如公式
("x){[($y)("z)P(x,y,z)]®("u)Q(x,u)}
可按下列步骤转换成标准形式:
(1)消去蕴含符号
("x){Ø[($y)("z)P(x,y,z)]Ú("u)Q(x,u)}
(2)把否定符号Ø移到每个谓词符号的前面
("x){("y)($z)[ØP(x,y,z)]Ú("u)Q(x,u)}
(3)消去存在量词
("x){("y)[ØP(x,y,f(x,y))]Ú("u)Q(x,u)}
(4)将公式化为前束形,并略去全称量词
ØP(x,y,f(x,y))ÚQ(x,u)
(5)恢复蕴含式
P(x,y,f(x,y))®Q(x,u)
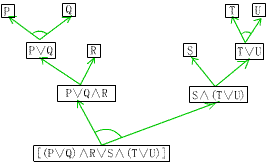
规则可以作用于与或图,形成一个新的与或图。我们先说明没有变量的情况。例如有规则
S®(XÙY)ÚZ

图1
与或图如图1所示,这条规则可应用于该图的S叶结点上形成图2。图中两个标有S的结点之间的弧称为匹配弧。注意到,新生成的与或图既表示了原图表示的事实表达式,又表示了由规则推导出的所有新的事实表达式。
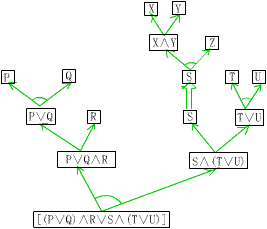
图2
首先考察上述规则能够推导出那些子句。规则的子句形式为
ØSÚXÚZ
ØSÚXÚZ
由图1可以看出,事实表达式中能够与规则子句进行归结求解的子句为
SÚR 和 SÚPÚQ
应用归结原理,可得到下列子句
RÚXÚZ RÚYÚZ
PÚQÚXÚZ PÚQÚYÚZ
所有这4个子句全在图2中表达出来了。应用一条规则获得了几个归结式,因此直接法的效率比较高。
图中的结点S应用一条规则后不再是叶结点,但仍是文字结点,还可对该结点应用其他规则。我们规定一个与或图表示的子句集对应于结束于文字结点上的解图集。这样,应用规则后得到的与或图既表示了原与或图所表示的表达式,也表示了新产生的表达式。