
含有变量的情况
在正向演绎系统中,我们假设事实和规则中所有的存在量词量化的变量,均已用Skolem函数替代,表达式中尚存的变量都是全称量词量化的变量。对于目标公式,我们要求所有全称量词量化的变量都被Skolem函数替代,省略存在量词,表达式中尚存的变量都认为是存在量词量化的变量。对目标公式的做法是与归结反演系统中取目标公式的否定相对应的。
目标表达式的形式仍为文字的析取形式。由于存在量词的性质:
($x)[X1(x)ÚX2(x)]≡($x)X1(x)Ú($y)X2(y)
因此,目标公式中各析取文字的变量可以改名,从而使用不同的变量符号。
例如考虑如下问题:
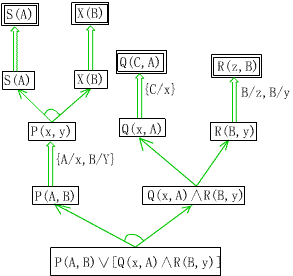
事实表达式: P(A,b)Ú[Q(x,A)R(b,y)]
规则: P(x,y)®S(x)ÚX(y)
目标公式: Q(c,A)ÚR(z,b)ÚS(A)ÚX(b)
事实表达式和规则中的变量都是全称量词量化的,目标公式中的变量则是存在量词量化的,它们都满足上面提出的要求。事实表达式的与或图如图1所示,应用规则后的与或图如图2所示,图中还画出了与目标文字(用双框表示)的匹配。从表面上看,图中包括两个在目标文字上结束的解图,对应的子句为
S(A)ÚX(b)ÚQ(c,A)
S(A)ÚX(b)ÚR(z,b)


图1有变量的事实表达式的与或图 图2 有变量的规则应用与目标匹配图
但事实上第一个子句是不成立的,因为该解图中使用的置换{A/x,b/y}和{c/x}是不一致的.但是,第二个子句对应的解图中,使用的置换{A/x,b/y}和{b/z,b/y}是一致的,将两个置换的合一复合{A/x,b/y,b/z}作用于第二个子句得到的例S(A)ÚX(b)ÚR(b,b)才是最后得到的子句。
总之,我们只能考虑那些结束在目标结点上的具有一致的匹配弧置换的解图—— 一致解图,并以对该解图对应的子句应用置换的合一复合所得到的例作为解答语句。下面给出置换的一致性和置换的合一复合的定义。
定义 设有一个置换集U={u1,u2,...,un},每个ui是一个置换对的集合
ui={ti1/vi1,...,tim(i)/vim(i)}
其中t为项,v为变量,令
U1=(v11,...,v1m(1),...,vn1,...,vnm(n))
U2=(t11,...,t1m(1),...,tn1,...,tnm(n))
置换U称为一致的,当且仅当U1和U2是可合一的,而U的合一复合u=mgu(U1,U2)。
例如有置换u1={x/y,x/z}和u2={A/z}
令 U1=(y,z,z)
U2=(x,x,A)
可以求得U1和U2的最小合一者为
u=mgu(U1,U2)={A/x,A/y,A/z}
因此置换u1和u2是一致的,且合一复合为u。
可以证明,合一复合运算是可结合的、可交换的,所以一个解图的合一复合与匹配弧的次序无关。
为了避免不必要的不一致,应用中应注意以下几点:
(1)多次应用同一规则时,每次应把变量改名。
(2)多次应用同一目标文字时,每次应把变量改名。
(3)当存在一个结束于目标文字上的一致解图时,证明成功的结束。
下面是一个例子作为对正向演绎系统讨论的结束。
事实:Fido barks and bites or Fido is not a dog(Fido吠且咬人,或者Fido不是狗) 。
ØDOG(FIDO)Ú[barKS(FIDO)ÙbITES(FIDO)]
规则:All terriers are dogs(所有猎犬都是狗)。
R1:ØDOG(x)®ØTERRIER(x)(这里使用逆否形式)
Anyone who barks is noisy(吠叫的都是喧闹的)。
R2: barKS(y)®NOISY(y)
证明目标:There exits someone who is not a terrier or who is noisy (存在某物或者不是猎犬或者是喧闹的)。
ØTERRIER(z)ÚNOIZY(z)
问题的与或图如图3所示。结束于目标结点的一致解图有置换{FIDO/x},{FIDO/y},{FIDO/z},这些置换的一致复合为{FIDO/x,FIDO/y,FIDO/z},因此得到证明。合一复合于一致解图对应的子句得到
ØTERRIER(FIDO)ÚNOIZY(FIDO)
它是目标公式的一个例,可作为解答语句。

图3 猎犬问题的与或图
习题
“猴子和香蕉问题”经常用来说明人工智能中关于规划生成的概念。这个问题可以叙述如下:一个猴子在有一个箱子和一串香蕉的房间里,天花板上吊着一串香蕉,猴子伸手抓不到。猴子试图得到这香蕉。
用F规则表示这个问题,使规划生成系统可以生成包括下列动作的规则:走向箱子,把箱子推到香蕉底下,爬上箱子,得到香蕉。