控制策略
我们先看下面的例子
设有以下事实:
F1: “FIDO是一只狗”。 DOG(FIDO)
F2: “FIDO不叫”。 ØbarKS(FIDO)
F3: “FIDO摇尾巴”。 WAGS-TaiL(FIDO)
F4: “MYrtLE喵喵叫”。 MEOWS(MYrtLE)
规则集合如下
R1:“摇尾巴的狗是友好的”。
[WAGS-TaiL(x1)ÙDOG(x1)]®FRIENDLY(x1)
R2:“友好且不叫的是不令对方害怕的”。
[FRIENDLY(x2)ÙØbarKS(x2)]®ØAFRaiD(y2,x2)
R3:“狗是动物”。
DOG(x3)®ANIMAL(x3)
R4:“猫是动物”。
cAT(x4)®ANIMAL(x4)
R5: “喵喵叫的是猫”。
MEOWS(x5)®cAT(x5)
证明目标:“是否存在一只猫和一只狗,使这只猫不怕这只狗”。
($x)($y)[cAT(x)ÙDOG(y)ÙØAFRaiD(x,y)]
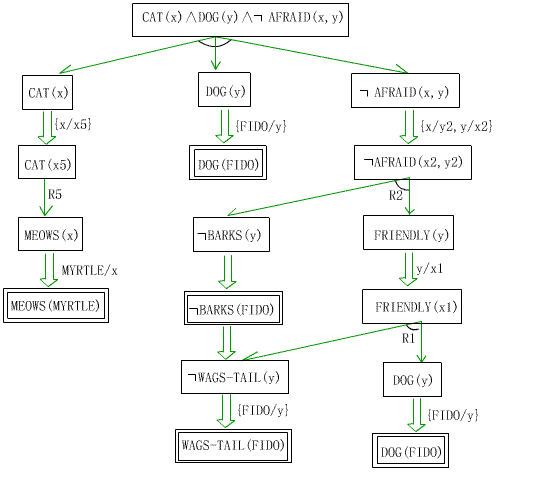
逆向系统的一个一致解图如下图所示。解图中匹配弧上所标记的置换包括:{x/x5},{MYrtLE/x}、{FIDO/y}、{x/y2,y/x2}、{FIDO/y}、{y/x1} 、{FIDO/y}和{FIDO/y}。这些置换的合一复合为{MYrtLE/x5,MYrtLE/x,FIDO/y,MYrtLE/y2,FIDO/x2,FIDO/x1},这个合一复合作用于目标表达式就得到解答语句:
cAT(MYrtLE)ÙDOG(FIDO)ÙØAFRaiD(MYrtLE,FIDO)

逆向系统的一致解图示例
由此我们归纳控制策略如下:
演绎系统的目标是在搜索图中建立一个一致解图。基本的策略是先寻找候选解图,再验证它的一致性。如果不一致,再寻找另一个解图,直到找到一个一致解图为止。
一个比较好的策略是在生成了局部解图时就检验其一致性。如果局部解图就不一致,就可以立即放弃生成该解图,因此减少了搜索量。
另一个策略是预先计算规则所有可能的匹配并存贮产生的各个置换,建立一个称为规则连接图的结构。在推理过程中可直接使用规则连接图,从而提高了效率。在规则集合比较小时,这个策略是适宜的。
以上策略对正向演绎系统也是适用的。
习题
1、“猴子和香蕉问题”经常用来说明人工智能中关于规划生成的概念。这个问题可以叙述如下:一个猴子在有一个箱子和一串香蕉的房间里,天花板上吊着一串香蕉,猴子伸手抓不到。猴子试图得到这香蕉。
用b规则表示这个问题,使规划生成系统可以生成包括下列动作的规则:走向箱子,把箱子推到香蕉底下,爬上箱子,得到香蕉。
2、我们来考虑下列一段指示:Tony、Mike和John属于Alpine俱乐部,Alpine俱乐部的成员不是滑雪运动员就是登山运动员。登山运动员不喜欢雨,而且任何不喜欢雪的人不是滑雪运动员。Mike讨厌Tony所喜欢的一切东西,而喜欢Tony所讨厌的一切东西。Tony喜欢雨和雪。
以谓词演算语句的集合表示这段知识,用逆向系统回答问题:“有没有Alpine俱乐部的一个成员,他是一个登山运动员但不是一个滑雪运动员呢?”