不确定性问题的代数模型
一个不确定性知识推理包括如下的算法:
算法1:根据规则前提E的不确定性c(E)和规则强度f(H,E)求出假设H的不确定性c(H),即定义函数g1,使得
c(H)=g1[c(E),f(H,E)]
算法2:根据分别由独立的证据E1和E2所求得的假设H的不确定性c1(H)和c2(H),求出证据E1和E2的组合所导致的假设H的不确定性c(H),即定义函数g2,使得
c(H)=g2[c1(H),c2(H)]
算法3:根据两个证据E1和E2的不确定性c(E1)和c(E2),求出证据E1和E2的合取的不确定性,即定义函数g3,使得
c(E1ÙE2)=g3[c(E1),c(E2)]
算法4:根据两个证据E1和E2的不确定性c(E1)和c(E2),求出证据E1和E2的析取的不确定性,即定义函数g4,使得
c(E1ÚE2)=g4[c(E1),c(E2)]
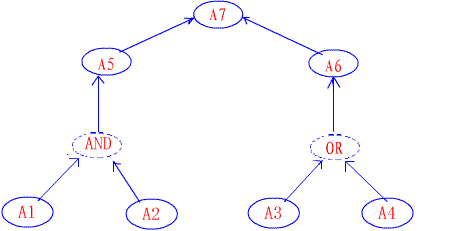
观察下图所示的推理网络。

设A1、A2、a3、A4为原始证据,即已知证据A1、A2、a3、A4的不确定性分别为c(A1)、c(A2)、c(a3)、 c(A4)。求A5、A6、A7的不确定性。
问题的求解过程为:
1、由证据A1和A2的不确定性c(A1)和c(A2),根据算法4求出A1和A2析取的不确定性c(A1ÚA2)。
2、由A1和A2析取的不确定性c(A1ÚA2)和规则R1的规则强度f1,根据算法1求出A5的不确定性c(A5)。
3、由证据a3和A4的不确定性c(a3)和c(A4),根据算法3求出a3和A4合取的不确定性c(A1ÙA2)。
4、由a3和A4合取的不确定性c(A1ÙA2)和规则R2的规则强度f2,根据算法1求出A6的不确定性c(A6)。
5、由A5的不确定性c(A5)和规则R3的规则强度f3,根据算法1求出A7的其中一个不确定性c1(A7)。
6、由A6的不确定性c(A6)和规则R4的规则强度f4,根据算法1求出A7的另外一个不确定性c2(A7)。
7、由A7的两个根据独立证据分别求出的不确定性c1(A7)和c2(A7),根据算法2求出A7最后的不确定性
c(A7)。
c、不确定推理的语义
综上所述,对于一个不确定推理问题应指出不确定性表示和推理的含义。基于概率论的方法能较好的解决这个问题。
如规则强度f(b,A)可理解为当证据A为真时,对假设b为真的一种影响程度;而c(A)可理解为A为真的程度,即对于f(b,A)和c(A),应给出:
对于f(b,A)而言:
(1)A为真则b为真,这时f(b,A)=?
(2)A为真则b为假,这时f(b,A)=?
(3)A对b没有影响时,这时f(b,A)=?
对于c(A)而言:
(1)A为真时,c(A)=?
(2)A为假时,c(A)=?
(1)对A一无所知时,c(A)=?
习题
1、分别以不精确性、不完全性、模糊性和非单调性举例说明现实世界知识的不确定性。