上承

  在MYcIN中，还是用了另一个基本概念——确定性因子cF，它的作用是把Mb和MD组合在一起，cF的定义为：

          cF(H,E)=Mb(H,E)-MD(H,E)

    根据Mb、MD和cF的定义，我们可以导出如下性质：

 根据Mb、MD和cF的定义，我们可以导出如下性质：

1、Mb与MD的互斥性

         当 Mb(H,E)>0时，MD(H,E)=0

         当MD(H,E)>0时， Mb(H,E)=0

        Mb与MD的互斥性表明对同一个证据E，可能同时既增加对H的信任增长度，又增加对H的不信任增长度，即不可能因为证据E的出现，既使P(H|E)>P(H)，又使P(H|E)<P(H)。

2、假设的互斥性

       若对于同一证据有n个互不相容的假设Hi(i=1,2,...,n)，则

    仅当证据E在逻辑上蕴含某个假设Hi时，上式的等式才成立。

    根据性质（1）可以直接用概率值来表示：

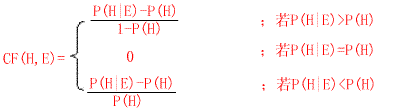
    3、值域

    Mb、MD和cF的值域为：

         0≤Mb(H,E)≤1 

         0≤MD(H,E)≤1  

         -1≤cF(H,E)≤1

    4、证实的情况

    5、不证实的情况

    若Mb(H,E)=0，说明E的存在证实不了H，或者是E与H独立，或者是E否认H。

    若MD(H,E)=0，说明E的存在不否认H，或者是E与H独立，或者是E证实H。

    若cF(H,E)=0，表示E与H独立。

    6、cF不同于概率P

    从上面的定义可以看出，确定性因子法中cF与概率P有一定的对应关系，但又有所区别，因为对于概率恒有：

    P(H|E)+P(ØH|E)=1

而  cF(H,E)+cF(ØH,E)=0

    由此可见，确定性因子法的cF概念与概率P的概念是不同的。   

  习题

  1、简要叙述几种主要的不确定推理方法及个自的优缺点。

  2、构造一个不确定性知识系统一般要涉及那几个问题？

                                    返回