不确定推理算法

    根据证据E分三种情况：

    1、E肯定存在的情况

    在证据E肯定存在时有cF(E)=1，那么结论H的确定性因子为真，即有

        cF(E)=cF(H,E)

    2、E不是肯定存在的情况

    在客观的现实世界中，对证据的观察往往也是不确定的。除此之外，证据E可能还是另一条规则的结论，

这时也常常是不确定的。在这种情况下，结论H的确定性因子cF(H)不仅取决于规则的确定性因子cF(H,E)，

而且还取决于证据E的确定性因子cF(E)。计算公式为

        cF(H)=cF(H,E)*max{0,cF(E)}

    3、证据是多个条件的逻辑组合的情况

    我们分三种情况进行讨论

    （1）证据是合取连接

     若系统有规则形如

                   IF E1 AND E2 AND ... AND En THEN H(x),

     那么，有cF(E)=cF(E1 AND E2 AND ...AND En)

                  =min{cF(E1),cF(E2),...,cF(En)}

    （2）证据是析取连接

     这时，E=E1 OR E2 OR ... OR En，有

             cF(E)=cF(E1 OR E2 OR ...OR En)

                  =max{cF(E1),cF(E2),...,cF(En)}

    （3）两条规则具有相同结论的情况

     若有两条规则分别是

           IF E1 THEN H(cF(H,E1))

           IF E2 THEN H(cF(H,E2))

那么首先分别计算出cF1(H)和cF2(H)：

           cF1(H)=cF(H,E1)*max{0,cF(E1)}

           cF2(H)=cF(H,E2)*max{0,cF(E2)}

    然后用公式

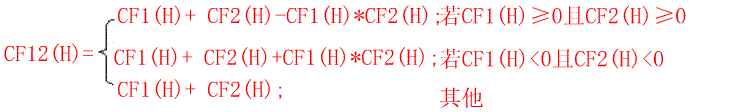
计算出由E1和E2组合而导出的确定性因子cF12(H)。

                                返回