不确定推理算法举例(确定因子法)

    例6-1 下面通过一个例子说明该方法的推理过程。

    例如有如下的推理规则：

    rule 1:IF E1 THEN H(0.9)

    rule 2:IF E2 THEN H(0.7)

    rule 3:IF E3 THEN H(-0.8)

    rule 4:IF E4 AND E5 THEN E1(0.7)

    rule 5:IF E6 AND (E7 OR E8) THEN E2(1.0)  

形成的推理网络如图5-2所示。

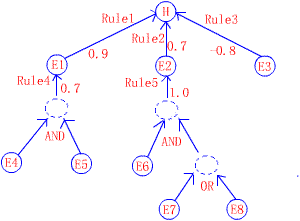
   图5-2 规则形成的推理网络

在图5-2中，E3、E4、E5、E6 、E7和E8为原始证据，其确定性因子由用户给出，假定它们的值为：

    cF(E3)=0.3  cF(E4)=0.9   cF(E5)=0.6   

    cF(E6)=0.7  cF(E7)=-0.3   cF(E8)=0.8

系统的求值顺序是先求出cF(E1)、cF(E2)和cF(E3)，然后再求cF(H)。

    cF(E1)=0.7*max{0,cF(E4 AND E5)}

          =0.7*max{0,min{cF(E4),cF(E5)}}

          =0.7*max{0,min{0.9,0.6}}

          =0.7*0.6

          =0.42

    cF(E2)=1*max{0,cF(E6 AND(E7 OR E8))}

          =1*max{0,min{cF(E6),max{cF(E7),cF(E8)}}}

          =1*max{0,min{cF(E6),max{-0.3,0.8}}}

          =1*max{0,min{0.7,0.8}}

          =1*0.7

          =0.7

    cF(E3)=0.8

    cF1(H)=0.9*max{0,cF(E1)}

          =0.9*max{0,0.42}

          =0.9*0.42

          =0.38

    cF2(H)=0.7*max{0,cF(E2)}

          =0.7*max{0,0.7}

          =0.7*0.7

          =0.49

    cF3(H)=-0.8*cF(E3)

          =-0.8*0.3

          =-0.24

     因为cF1(H)>0且cF2(H)>0

     所以cF12=cF1(H)+cF2(H)-cF1(H)*cF2(H)

             =0.38+0.49-0.38*0.49=0.6838

    又因为cF1(H)>0，cF2(H)<0

     所以cF123=cF(H)=cF12(H)+cF3(H)

             =0.6838-0.24=0.4438

    所以由此推出结论H的确定性因子cF(H)=0.4438。

  习题

  设某问题求解用到以下的推理规则：

  rule1: IF E1 THEN H1(0.9)

  rule2: IF E2 THEN H1(0.5)

  rule3: IF E3 and E4 THEN E1(0.8)

  rule4: IF E5 and E6 THEN E2(1.0)

  试画出其推理网络图，用确定因子法求出H1的可信度cF(H1,E1&E2),假定已知在当前观察有

  cF(E3)=0.3，cF(E4)=0.4，cF(E5)=0.5，cF(E6)=0.6。

                                             返回