D-S方法应用举例
例 在专家系统的推理过程中,原始证据的确定性是由用户回答的。例如,有以下的推理规则:
rule1 IF E1 AND E2 THEN A={a1,a2},cF={0.3,0.5}
rule2 IF E3 AND (E4 OR E5) THEN N={n1},cF={0.7}
rule3 IF A THEN H={h1,h2,h3},cF={0.1,0.5,0.3}
rule4 IF N THEN H={h1,h2,h3},cF={0.4,0.2,0.1}
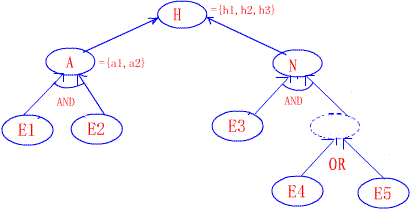
这些规则形成的推理网络如下图

推理网络图
设用户给出的原始证据的确定性是
cER(E1)=0.8,cER(E2)=0.6,cER(E3)=0.9,cER(E4)=0.5,cER(E5)=0.7 并假定:|U|=20
解:下面依次求出A的确定性cER(A),N的确定性cER(N)和H的确定性cER(H)。
1.求cER(A)
先求出rule1条件部分的确定性,利用公式有
cER(E)=cER(E1 AND E2)
=min{cER(E1),cER(E2)}
=min{0.8,0.6}=0.6
再求假设A的基本概率赋值函数m为
m({a1},{a2})=(0.6*c1,0.6*c2)
=(0.6*0.3,0.6*0.5)
=(0.18,0.3)
于是有
bel(A)=m({a1})+m({a2})=0.18+0.3=0.48
Pl(A)=1-bel(ØA)=1-0=1
f(A)=bel(A)+(|A|/|U|)[Pl(A)-bel(A)]
=0.48+(2/20)*(1-0.48)=0.53
cER(A)=MD(A,E')*f(A)=1*0.53=0.53
其中MD(A,E')是因为E'为已证实的命题(此例中为A的前提E1和E2均已证实)。
2.求cER(N)
利用公式,有
cER(E)=cER(E3 AND (E4 OR E5))
=min{cER(E3),max{cER(E4),cER(E5)}}
=min{0.9,max{0.5,0.7}}=0.7
m({n1})=(0.7*c1)=(0.7*0.7)=0.49
bel(N)=m({n1})=0.49
Pl(N)=1-bel(ØN)=1
f(N)=bel(N)+(|N|/|U|)[Pl(N)-bel(N)]
=0.49+(1/20)*(1-0.49)=0.52
cER(N)=MD(N,E')*f(N)=1*0.52=0.52
3.求cER(H)
利用公式,有
m1({h1},{h2},{h3})=(cER(A)*c1,cER(A)*c2,cER(A)*c3)
=(0.53*0.1,0.53*0.5,0.53*0.3)
=(0.053,0.265,0.159)
m1(U)=1-(0.053+0.265+0.159)=0.524
m2({h1},{h2},{h3})=(cER(N)*c1,cER(N)*c2,cER(N)*c3)
=(0.52*0.4,0.52*0.2,0.52*0.1)
=(0.208,0.104,0.052)
m2(U)=1-(0.208+0.104+0.052)=0.636
然后求出m1与m2的正交和m1⊕m2⊕。为此,先求出 K-1
K-1=m1({h1})*m2({h1})+m1({h1})*m2({U})+m1({h2})*m2({h3})
+m1({h2})*m2({U})+m1({h3})*m2({h3})+m1({h3})*m2({U})
+m1({U})*m2({h1})+m1({U})*m2({h2})+m1({U})*m2({h3})+m1({U})*m2({U})
=0.053*0.208+0.053*0.636+0.263*0.104+0.265*0.636+0.159*0.052
+0.159*0.636+0.524*0.208+0.524*0.104+0.524*0.052+0.524*0.636
≈0.874
于是
m({h1})=(1/0.874)*[m({h1})*m2({h2})+m1({h1})*m2({U})+m1({U})*m2({h1})]
=(1/0.874)*[0.053*0.208+0.053*0.636+0.524*0.208]
≈0.176
同理,我们可以计算得到:
m({h2})≈0.299
m({h3})≈0.157
而
m(U)=1-(0.176+0.299+0.157)=0.368
bel(H)=m({h1})+m({h2})+m({h3})
=0.176+0.299+0.157=0.632
Pl(H)=1
f(H)=bel(H)+(|H|/|U|)[Pl(H)-bel(H)]
=0.632+(3/20)*(1-0.632)=0.687
cER(H)=MD(H,E')*f(H)=0.687
至此,我们求出了H的确定性为0.687。