命题模糊命题的转换规则

     1、  修正规则

修正规则表示为

如果   Y is F→Ⅱ_y=F

那么   Y is mF→Ⅱ_y=F⁺

其中m是模糊修饰语，F⁺是m对F的一个修正结果。

当m=not(“不”、“非”等)，那么有F⁺=~F，即

u_F+(x)= 1-u_f(x)x∈[0,1]

当m=Very(“很”、“非常”等)，那么有F⁺=F²，即

u_f+(x)=u²_F(x)x∈[0,1]

当m=more of less(“有些”、“稍微”等)，那么有F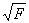⁺= ，即

u_f+(x)=   X∈[0,1]

    2、 合取、析取和蕴含规则  

设有命题

Y is F→Ⅱ_y=F

Z is G→Ⅱ_z=G

其中F和G分别是模糊变量x₁和x₂的模糊子集。那么两命题的合取

（Y is F）∧(Z is G)→Ⅱ_(y,z)=F×G

其中

u_F×G(x_1,x₂)   u_F(x₁)∧u_G(x­₂)

而两命题的析取

（Y is F）∨(Z is G) →Ⅱ_(y,z)=F^*UG^*

其中

F^*    F×x₂,  G^*    x₁×G  

UF^*U_G^*(x_1,x₂)=uf(x₁) ∨uG(x₂)

进而两命题的蕴含

（Y is F）→(Z is G) →Ⅱ_(z∣y)=F^*’  G^*

其中Ⅱ_(z∣y)表示给定Y后，Z的条件可能性分布；  表示有界和，且定义为

uf^*’  G^*(x₁,x₂)=1∧(1-Uf(X₁)+Uc(X₂))  

        3、 量化规则           

如果X={x₁,x₂,…,x_n},Q是一个模糊量词，且

Y is F→U_Y=F

那么命题“QY are F”可以转换成如下形式

Ⅱ_cOUNT（F_）=Q

其中

court(F) =

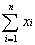
4、真值量化规则

设T是一个模糊真值，一个真值量化命题可以表示为“Y is F is T”,这类命题的转换规则可以表示成如下的形式

Y is F is T→Ⅱ_Y=F⁺

其中

   =                              

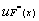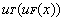
　　　　　　　　　　　　　　　返回