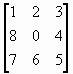| 概述 |
| 逻辑表示法 |
| 规则表示法 |
| 语义网络表示法 |
| 框架表示法 |
| 面向对象表示法 |
| 逻辑 规则 语义 框架 对象 |
|
八数码游戏 |
在一个有三行三列共九样子的棋盘上,在共中八个格子上放着写有数字的方块。游戏的方法是:每次把空格旁边的一个数字方块移到空格去,目的是将初始的布局(状态)改变成目标布局(状态)。如图所示给出了一个初始布局和一个目标布局。问题是:确定一个方块移动的序列,使初始布局改变为目标布局。
|
|
|||||||||||||||||||
| 初始布局 | 目标布局 |
把这个问题转化为产生式系统的步骤:
第一步:综合数据库。把棋盘的布局用一个33的矩阵来表示,称为状态描述。初始的综合数据库就是问题的初始状态描述,每移动一个数字方块,状态描述就变化一次,我们把所有存储在计算机中的产生过的状态描述称为综合数据库。
|
|
|
|
| 初始布局对应矩阵 | 目标布局对应矩阵 |
第二步:规定产生式规则。为简化起见,我们把移动数字方块表述为移动空格,这样移动空格的不同方向就构成了不同的产生式规则。由于每个空格移动方向都有先决条件,例如空格上移的先决条件就是空格不在最上边的一行,因此产生式规则可表示为:
(1) if 空格不在最上一行,then 空格上移
(2) if 空格不在最下一行,then 空格下移
(3) if 空格不在最左一列,then 空格左移
(4) if 空格不在最右一列,then 空格右移
第三步:确定控制系统。控制系统的目标是不断选择合适的产生式规则作用于综合数据库,改变综合数据库的状态,直至产生了目标描述为止,这时,施行过的产生式规则的序列就是问题的解。显然就八数码游戏而言,解不是唯一的,因此我们还可以加入一些约束条件,例如要求一个移动方块次数最少的解。
|
2、传教士和野人问题 |
河的左岸有N个传教士和N个野人准备渡河,河岸有一条渡船,每次最多可供K人渡河。为安全起见,在任何时刻,河两岸以及船上的野人数目不得超过付教士的数目。求渡河的方案。
下面将N=3,K=2的情况表示成产生式系统要求的形式。由于河的两边教士的总数、野人的总数和船的总数是固定的,因此只需表示河的一边的状态就可以了。为些设左岸的传教士数目为m,左岸的野人数目为c,左岸的渡船数目为b(b取0或1)。这样,渡河过程的状态可以用三元组(m,c,b)表示。问题的初始状态和目标状态可表示为(3,3,1)和(0,0,0)
对于N=3的情况,状态空间总数为4*4*2=32。但是为了满足约束条件,只有满足下列条件之一时,状态才是合法的:(1)m=0,(2)m=3,(3)m=c
系统的综合数据库记录上述的状态描述。产生式规则应对应于摆渡操作。设P表示将m个传教士和c个野人从左岸关到右岸的规则,Q表示将m个传教士和c个野人从右岸送到左岸的规则,则规则集合为:
R={P01、P10、P11、P02、P20、Q01、Q10、Q11、Q02、Q20}
考虑到约束条件,规则集应表示如下:
| 规 则 | 条 件 | 动 作 |
| P01 | b=1,(m=0,或m=3),c |
b=0,c=c-1 |
| P10 | b=1,(m=1,c=1或m=3,c=2) | b=0,m=m-1 |
| P11 | b=1,m=c,c |
b=0,m=m-1,c=c-1 |
| P02 | b=1,(m=0或m=3),c |
b=0,c=c-2 |
| P20 | b=1,(m=3,c=1或m=2,c=2) | b=0,m=m-2 |
| Q01 | b=0,(m=0或m=3),c |
b=1,c=c+1 |
| Q10 | b=0,(m=2,c=2或m=0,c=1) | b=1,m=m+1 |
| Q11 | b=0,m=c,c |
b=1,m=m+1,c=c+1 |
| Q02 | b=0,(m=0或m=3),c |
b=1,c=c+2 |
| Q20 | b=0,(m=0,c=2或m=1,c=1) | b=1,m=m+2 |
|
传教士和野人问题的规则表 |
||