| 概述 |
| 逻辑表示法 |
| 规则表示法 |
| 语义网络表示法 |
| 框架表示法 |
| 面向对象表示法 |
| 逻辑 规则 语义 框架 对象 |
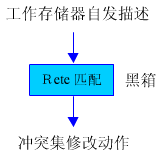
Rete快速匹配算法
Rete算法首先是由c.L.Forgy在1979年实现的。该算法是一个快速的模式匹配算法,它通过存储关于规则的信息而获得速度。
|
模式匹配的基本概念 |
1、可满足规则:一个规则称为可满足的,若规则的每一模式均能在当前工作存储器中找到可匹配的事实,且模式之间的同一变量能取得统一的约束值。形式化地说,规则
|
if P1,P2,…Pm then A1,A2,…An |
称为可满足的,若存在一个通代σ,使得对每一个模式Pi,在工作存储器中有一个元素Wi满足
Piσ=Wi i=1,2,3 …m
这里,σ作用在某个模式的结果称为模式实例,σ作用在整个规则的结果称为规则实例。在专家系统中,可满足的规则称为标志规则。
2、冲突集:由全体规则实例构成的集合称为冲突集。也称为上程表。
3、模式匹配算法的任务是:给定规则库,根据工作存储器的当前状态,通过与规则模式的匹配,把可满足规则送入冲突集,把不可满足的规则从冲突集中删去
|
Rete算法的基本思想 |
一、Rete算法快速匹配的重要依据是:(1)时间冗余性.工作存储器中的内容在推理过程中的变化是缓慢的,即在每个执行周期中,增删的事实只占很小的比例,因此,受工作存储器变化而影响的规则也只占很小的比例。由产生式系统的折射性,只要在每个执行周期中记住哪些事实是已经匹配的,需要考虑的就仅仅是修改的事实对匹配过程的影响。(2)结构相似性.许多规则常常包含类似的模式和模式组。
|
|
|
Rete算法功能图 |
二、Rete算法的基本思想是:保存过去匹配过程中留下的全部信息,以空间代价来换取产生式系统的执行效率。
|
Rete匹配网络结构 |
Rete算法的核心是建立Rete匹配网络结构。其由模式网络和连接网络两部分构成。其中,模式网络记录每一模式各域的测试条件,每一测试条件对应于网络的一个域结点,每一模式的所有域结点依次连起来,构成模式网络的一条匹配链。
|
Rete匹配网络过程 |
Rete网络匹配过程由模式网络上的模式匹配和连接网络上的部分匹配构成。在模式网络的机器内部表示中,我们把共享一个父结点的所有结点表示成一条共享链。同时,把每一模式匹配链中的结点表示成一条下拉链,于是,每一结点由共享链和下拉链指向其后继结点,模式网络就是一棵可以使用典型遍历算法进行测试的二叉树。例如:
有规则
(defrule exa-2
(match ?y red)
(data ![]() green
?y)
green
?y)
(data ?y ?y)
(other ?y)
=>)
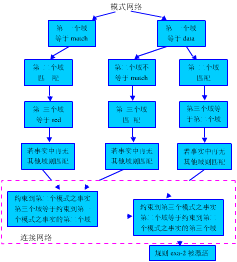
则此规则对应的模式网络和连接网络图示如下:
|
|
|
规则exa-2对应的模式网络和连接网络示意图 |