第3章 市场需求分析
3.1消费效用与需求
3.1.1总效用与边际效用
1.效用
效用是消费者从消费的商品和劳务中所感受到的满足程度。效用这一概念与人的欲望是联系在一起的,它是消费者对商品满足自己的欲望的能力的一种主观心理评价。效用因人、因时、因地而不同,由于同一物品对两个不同的人来说其效用可能大不一样,因而由两个不同的人来对同一物品的效用作比较是不可能的,效用大小的比较只能由同一个人的主观感受来决定。
效用的大小一般用尤特尔(Util)表示。
2.边际效用
总效用是指消费者在一定时间内从一定数量的商品和劳务的消费中所得到的效用量的总和。
边际效用是指消费者在一定时间内从增加一单位商品的消费中所得到的效用量的增加量。
假定消费者对一种商品的消费数量为Q,则总效用函数为:TU=f(Q)
总效用函数表示消费者对一定量的物品或劳务产生的满足程度和其消费量之间的对应关系。
相应的边际效用函数为:![]()
当商品的增加量趋于无穷小,即![]() 时有:
时有:![]()
3.边际效用递减规律
边际效用递减规律是指随着消费者对某种商品消费数量的连续增加,消费者从增加的商品中所得到的效用的增加量是递减的。也就是说消费者在消费过程中得到的总效用在开始的时候不断增加,逐渐达到最大值,然后,又逐渐减少。但是,即使在总效用增加的时候,其增量也在逐渐减少,故边际效用趋于下降,并在总效用达到最大值以后变为负数,也就是对某种商品的消费超过一定量后,不但不能增加消费者的满足和享受,反而会引起痛苦的感觉。
商品数量和效用的关系如表3-1所示。
表 3-1 总效用和边际效用表
商品数量 Q |
总效用 TU |
边际效用 MU |
0 1 2 3 4 5 |
0 10 18 22 22 18 |
10 8 4 0 -4 |
4.等边际原则
在既定收入与商品价格条件下,为了实现效用最大化消费者应该使自己所购买的各种商品的边际效用与价格之比相等。或者说,消费者应使自己花费在各种商品购买上的最后一元钱所带来的边际效用相等。这是消费者购买商品时获得效用最大化的必要条件。
假定:消费者用既定的收入I购买n种商品,P1,P2……Pn分别为n种商品的既定的价格,λ为单位货币的边际效用。以X1,X2……Xn分别表示n种商品的数量,MU1,MU2……MUn分别n种商品的边际效用,则上述的消费者效用最大化的均衡条件可以用公式表示为:
约束条件 :
P1X1+P2X2+
…PnXn=1
消费者均衡的条件:
![]()
应该注意的是,上述均衡条件要求的是每一元钱所得到的边际效用相等,而不是每种商品的边际效用相等。
3.1.2消费者需求的最优组合
1.无差异曲线
无差异曲线表示能给消费者带来相同的效用水平和满足程度的两种商品的各种不同组合的点的轨迹。无差异曲线上的每一个点都代表一个商品组合,该商品组合能够给消费者带来相同的效用水平。
现在我们假定消费者消费苹果和梨,该消费者可以多消费苹果而减少梨的消费,或者少消费苹果而增加梨的消费,仍可得到同样的满足程度。假定苹果和梨相同效用水平的不同的组合如表3-2所示。
组合 |
梨( Y ) |
苹果( X ) |
A B C D |
10 6 4 2.5 |
1 2 3 4 |
表3-2 苹果和梨的不同组合
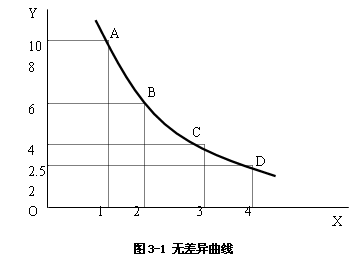
根据表3-2给出的苹果和梨的A,B,C,D四种不同数量的组合,每种组合提供的效用水平是相等的,或者说是无差异的。我们把表中的内容画在平面坐标图上,即可得到一条无差异曲线。用横轴表示苹果的数量,用纵轴表示梨的数量,每一组合均由图上的一点(如A,B,C,D)表示,连接各点的连线就是无差异曲线,如图4-4所示。
无差异曲线表明,该曲线上的任何一点的两种商品的不同组合所提供的总效用或总满足水平都是相等的,即无差异的,因此,消费者愿意选择其中任何一种组合。
2.预算线
预算线(budge line)又称消费可能线(consumption possibility line)或价格线(price line)。预算线表示在消费者收入和商品价格既定的条件下,消费者的全部货币收入所能购买到的两种商品的最大数量组合的集合。
假定消费者将其全部货币收入I用于购买两种商品X1,X2,X1商品的价格是P1,X2商品的价格是P2,则消费者的预算线方程可表示为:I=P1X1+P2X2
3消费者选择的最优组合
当一个理性的消费者面临一条既定的预算线和无数条无差异曲线时,只有既定的预算线与其中一条无差异曲线的相切点,才是消费者获得最大效用水平的均衡点。
如图3-2所示,消费者的预算线与无差异曲线的关系存在相交、相切和相离三种情况。
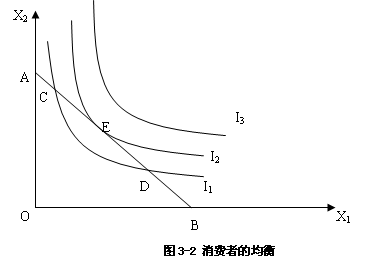
1.预算线AB与无差异曲线I1相交,交点为C,D两点。这两点虽然代表着一定的满足程度,但是它们并没有达到消费者支出允许的范围内所获取的最大的效用水平,因C,D移动到E点,可以在更高的满足水平上进行消费。
2.预算线AB与无差异曲线I3相离,虽然此时有较高的满足水平的存在,但是对消费者来说已经超过收入的许可,是一种可望而不可及的状态。
3.预算线AB与无差异曲线I2相切,切点为E点。E点同时在预算线AB及无差异曲线I2上,意味着它所代表的商品组合是消费者用现有的收入可以买到的,同时能给消费者带来最高水平的满足。显然,只要E点沿着预算线偏离原来的位置,它所代表的满足程度都将低于I2水平。因此,切点E代表既定收入条件下能给消费者带来最大满足程度和效用的商品组合。
3.2.需求的价格弹性
3.2.1.需求的价格弹性定义
需求的价格弹性(Price Elasticity of Demand)表示某种商品需求量对本身价格变化的反应程度。
需求的价格弹性系数就是需求量变化的相对量对价格变化的相对量的比值,公式为: 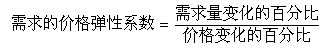
如果用Ed表示需求的价格弹性系数,用P表示价格, ΔP表示价格的变化量,Q和ΔQ分别代表需求量及需求的变化量,那么,需求的价格弹性公式一般形式为:
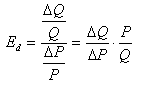
由于价格与需求量成反方向变动的关系,需求价格弹性系数为负,为了计算方便,一般都取其绝对值。
3.2.2.点弹性的计算
点弹性是指需求曲线上某一点的弹性(这时意味ΔQ和ΔP的量极微小,接近于零),点价格弹性的计算公式如下: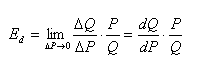
点弹性也可以用几何方法来求。用几何方法求,从一定意义上说,更为直观,更为简便。假如需求曲线为一条直线(见图3-3),按几何方法,则B点上的点弹性Ed=BC/AB。
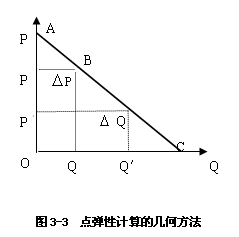
B点的点价格弹性Ed=BC/AB,其证明如下。
根据价格弹性的一般公式:
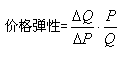
在图3-3中:
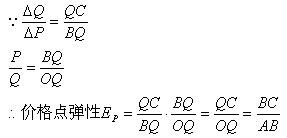
根据上述几何方法,可以直观地比较出在需求曲线的不同点上价格弹性的大小。
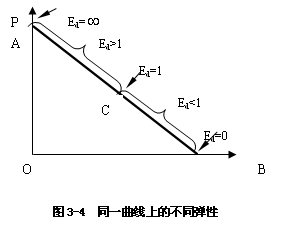
当需求曲线为一直线时,曲线斜率既定不变,但各点的需求弹性因位置不同而异,点的位置越高,其弹性越大;点的位置越低,其弹性越小。
3.2.3.弧弹性的计算
弧弹性是需求曲线上两点之间的平均弹性。如图3-5所示:
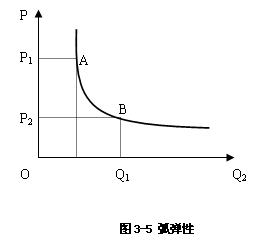
用中点公式计算的弧弹性如下:
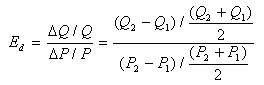
3.2.4.需求弹性的分类
1.Ed=0,需求完全无弹性;
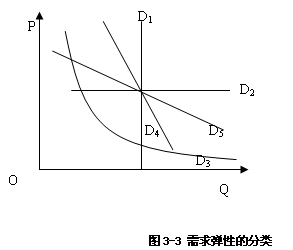
即无论价格如何变动,需求量都不会发生变动,商品的需求曲线是与纵轴平行的一条垂线,如图3-3的曲线D1所示。这在现实中是一种十分罕见的情况,通常认为像棺材、火葬场、特效药等,这样的商品或劳务接近于这种情况。
2.Ed
→∞,需求有无限弹性;
它表示在既定的价格水平上,需求量是无限的,而一旦高于既定价格,需求量即为零。说明商品的需求变动对价格变动非常敏感,如图3-3中D2,这也是现实生活中罕见的极端情况。
3.Ed=1,需求单位弹性;
它表示需求量与价格按同一比率发生变动,即价格每升降1%,需求量就相应减少或增加1%,其需求曲线为正双曲线,如图3-3中D3,这种情况在现实生活中也极为罕见。
4.Ed < 1,需求缺乏弹性;
它表示需求量变动的比率小于价格变动的比率,即价格每升降1%,需求量变动的百分率小于1%,生活必需品如粮食、食盐、蔬菜等大多属于此类型, 如图3-3中D4。
5.Ed>1,需求富有弹性。
它表示需求量变动的比率大于价格变动的比率。价格每升降1%,需求量变动百分率大于1%。奢侈品和价格昂贵的享受性劳务多属于这类商品,如图3-3中D5。
3.2.5.影响需求弹性的因素
1.商品的必需程度;
如果某种商品是日常生活必需品,那么需求弹性比较小。如盐、油、大米、燃料等,即使价格大幅度上涨,需求量也不会有很大的变化。一般情况下,奢侈品即非生活必需品价格弹性比较大,这些商品的需求对价格的变化比较敏感。“
2.商品的可代替程度;
某种商品的替代品越多,可代替程度越强,该商品的需求弹性就越大。该商品如果涨价,人们可能会选择其替代品,导致该商品的需求量大幅度减少。
3.在总支出中的比重;
如果一种商品在消费者总支出中占很小的份额,那么消费者对该商品的价格变化不会很敏感,因此需求弹性较小。如果该商品是一项较大的支出,那么价格变化后,消费者会对其需求重新慎重考虑,因而弹性较大。
4.商品用途的广泛性;
一般而言,一种商品的用途越多,其需求弹性就越大。例如:电力有广泛的用途,当其价格提高时,人们就会使用电力的主要用途如照明,而减少次要用途如电炊、空调的使用,必然会从多渠道影响对电力的需求,从而使需求量产生较大幅度减少。
5.商品耐用程度;
一般而言,使用寿命长的耐用品需求弹性大,而使用寿命短的非耐用品的需求弹性小。
此外,时间、地域差别、消费习惯、商品质量、售后服务等因素,也会影响需求的价格弹性。
3.2.6.需求价格弹性与总收益
总收益是指生产者在市场上出卖一定商品所获得的货币收入总额,它等于商品的价格乘以商品的销售量,
即:TR=P×Q,其中,TR表示总收益,P表示价格,Q表示销售量。
这里假定生产者的销售量等于市场对该商品的需求量。从公式可以看出,总收益是由价格P和需求量Q两个因素决定的,需求价格弹性恰恰就是测量Q对P变化的反应程度的概念。因此,总收益的变化与需求弹性的大小有关。
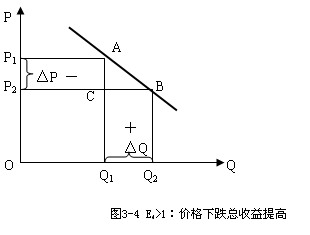
第一,富于弹性的商品(Ed >1),价格下降会提高总收益,价格上涨会减少总收益。
图3-8说明了这种情况:价格由P1下降到P2,销售量由Q1增加到Q2。OP1AQ1的面积代表原来的总收益,而OP2BQ2的面积是降价后的总收益。因为需求弹性大于1,需求曲线比较平坦,需求量上升的幅度大于价格下降的幅度,总收益不仅不会减少反而增加了,这就是我们常说的“薄利多销”的情况。如果价格由P2提高到Pl,则总收益就会减少。
第二,缺乏弹性(Ed < 1)的商品,价格下降减少总收益,价格提高增加总收益。
如图3-9说明这种情况:由于需求缺乏弹性,所以需求曲线比较陡峭。价格由P1下降到P2,而需求量由Q1仅增加到Q2, 需求量上升的幅度远小于价格下降的幅度,总收益不仅不会增加,反而会减少。相反当需求弹性不足时,如果提高价格,总收益不但不会减少,反而会增加。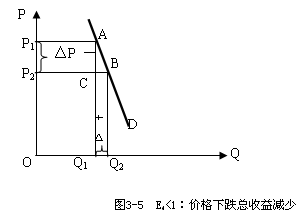
3.3 需求的交叉弹性
3.3.1需求的交叉弹性的计算
需求的交叉弹性表示在影响商品需求量的各因素包括该商品的价格(px)都是给定不变的条件下,另一相关商品Y的价格(Py)的变动引起的X的需求量(Qx)的变动程度。以Exy代表交叉价格弹性系数,则
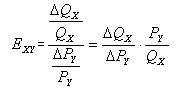
3.3.2需求的交叉弹性的经济含义
相关商品可以区分为替代品和互补品。如果两种商品在消费中存在互相替代的关系,它们就是替代品。消费者在购买两种具有替代关系的相关商品时,如果其中一种商品的价格上涨,另一种商品的需求量就会增加;反之,一种商品价格下降,另一种商品需求量就会减少。因此,如果商品x和商品y为替代品,交叉弹性系数必定是正值。
如果两种商品在消费中存在互相补充的关系,它们就是互补品。消费者在购买两种互补的相关商品时,如果其中一种商品价格上涨,另一种商品需求量就会减少;反之,一种商品价格下降,另一种商品需求量就会增加。因此,如果商品x和商品y为互补品,交叉弹性系数必定是负值。
3.4.需求的收入弹性
3.4.1需求的收入弹性的计算
在商品价格和影响需求量的其他因素不变的条件下,消费者收入I的变动将引起商品需求量(Q)的变动。因此,需求的收入弹性(EI)为: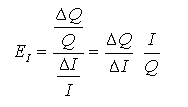
但是,收入提高时,并不是所有的商品的需求量都增加,收入下降时,也并非所有的商品的需求量都减少。
3.4.2需求的收入弹性的分类
根据EI 的大小,能够测定消费者收入变动对需求量变动的影响程度,而且可以将各种商品分为以下两大类:
1.正常品
一般来说,当消费者收入提高时,会增加对产品的需求量。当某种产品的需求量随收入的提高而增加,即需求量与收入成正方向变动时,叫正常商品(normal goods)。正常商品的EI >0,其中,又可以根据EI 是否大于1,将正常品分为奢侈品和必需品两种:
若EI >1,说明收入发生相对变动时,需求量变动更大。这种产品叫奢侈品(luxury goods);
若O < EI < 1,说明收入发生相对变动时,需求量变动较小。这种产品叫必需品(necessities)。
2.劣等品
有些产品,当消费者收入增加时,需求量反而减少。需求量随收入增加而减少的产品,叫劣等品(inferior goods)。劣等品的EI < 0。
案例1: 收入弹性与企业决策
对于一个实施多元化经营战略的企业来讲,选择什么产业进入是非常重要的,选择的标准可以很高,但最重要的因素之一是行业的成长性。因此,需求的收入弹性是一个很重要的参考数据。例如,1981年,美国通用电气公司(GE)的新总裁约翰?韦尔奇上任时,这家著名的跨国公司在全球已有300多家公司,约30万员工,分布十几个不同的行业,但GE所经营行业大部分是GNP产业,即这些产业的增长非常缓慢,只能与国民生产总值GNP的增长相当,如发电及变电设备制造业、电机电器业、火车头制造等,且竞争激烈。韦尔奇上任之后,将属于GNP产业的许多工厂关闭、转让、出售,把积蓄的资源转向航天航空、医疗器械、金融信息等产业,结果,短短几年,就使GE的年收益增长率超过了GNP增长率的3倍,使它在美国500家公司的排名由第10位上升到第1位。
案例2 需求收入弹性的实证结果(美国70年代末——80年代初)
商品 |
EY |
商品 |
EY |
燃 料 |
0.38 |
宗教和慈善事业 |
1.14 |
电、煤气 |
0.50 |
收音机、电视机 |
1.22 |
食 品 |
0.51 |
外出用餐 |
1.40 |
药 物 |
0.61 |
牙科服务 |
1.42 |
烟 草 |
0.64 |
书 籍 |
1.44 |
住院治疗 |
0.69 |
酒 类 |
1.54 |
医生服务 |
0.75 |
娱乐服务 |
1.57 |
服 装 |
1.02 |
新 车 |
2.45 |
理 发 |
1.03 |
家庭教育 |
2.48 |
住 房 |
1.04 |
|
|
电 话 |
1.13 |
|
|
案例3 需求收入弹性与价格弹性的综合考察
1979年,政府决定把猪肉的价格提高30%,在传统体制下,长达20多年价格没有大的变化,这是改革开放之初的一个重大步骤,政府有关部门为了不使城市居民因此造成生活水平的下降,给每个职工增发副食品补贴5元,这一涨价与补贴对需求会产生怎样的影响?
利用武汉市的季度数据估计了猪肉的需求函数,结果如下:
Q=0.3313P-0.8176*Y0.9635,相关背景为:
(Ⅰ) 需求的价格弹性EP=-0.8176,需求的收入弹性EY=0.9635。
(Ⅱ)当时的人均收入为每月35元,按每个职工负担一个家庭成员计算,副食品补贴每人每月2.5元,收入因补贴上升2.5/35=7% 。
(Ⅲ)每季人均消费猪肉约为8.6斤。
根据EP=-0.8176,价格上涨1%,需求下降0.8%左右,因此当价格上涨30%,需求下降24%左右,原来每季人均消费为8.6斤现将减少2.07斤猪肉的消费。根据EY=0.9635,收入上升1%,猪肉支出会增加0.96%,那么猪肉支出将增加6.8%左右,原来每季消费8.6斤,现应增加0.58斤消费。由此可知,比较2.07斤的减少量与0.58斤的增加量,实际每人每季会减少1.5斤猪肉的消费,平均每月减少半斤左右。
事实上,当时由于猪肉售价大幅度提高,又刺激了农民养猪的积极性,猪肉供应剧增,结果造成供过于求,不少地区只好一方面降价出售,一方面又压价购入,结果国家财政受到很大损失。
3.5供给弹性
3.5.1供给价格弹性的计算
同需求的价格弹性一样,供给的价格弹性测量价格变动引起的供给量变动的程度大小。供给的价格弹性系数ES被定义为:
或
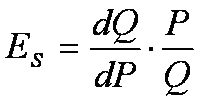
同需求的价格弹性一样,供给的价格弹性也有点弹性与弧弹性之分。上述的是点弹性公式,弧弹性公式为:
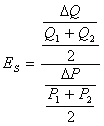
由于商品的供给量与价格的变动在一般情况下是同方向变动的,因此供给弹性系数为正值。
3.5.2供给弹性的类型
1.Es =0,供给完全无弹性;
其供给曲线是与纵轴平行的一条垂线,如图3-6中S1所示。极其稀缺、珍贵而无法复制的商品如土地、文物,接近于这类商品,不管价格如何,供给量始终不变。
2.Es=∞,供给弹性无穷大;
其供给曲线是一条与横轴平行的水平线,如图3-6中S2所示。表示在某一特定的价格下,厂商愿意提供任意数量的产品,而价格只要降低一点点,供给量就会骤然降至零。
3.Es =1,供给为单一弹性;
其供给曲线如图3-6中 S3所示。这也是现实生活中极为罕见的一种情况。
4.Es >1,供给富有弹性;
此时供给量变动的幅度大于价格变动的幅度。其供给曲线的形态比较平缓。如图3-6中S4所示。
5.Es < 1,供给缺乏弹性。
此时,供给量变动的幅度小于价格变动的幅度。其供给曲线的形状比较陡峭,如图3-6中S5所示。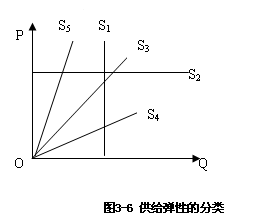
3.5.3.影响供给弹性的因素
1.进入和退出行业难易程度;
如果某一行业进入或退出壁垒很小,厂商可灵活根据价格和需求情况进入或退出该行业,则该产品的供给弹性较大,反之则相反。
2.供给者类别的大小;
如果考察的是单个生产者的供给弹性,那么一个人扩大产量的能力是有限的,供给弹性较小,如果考察的是一个行业的供给弹性,则要大得多,因为价格上涨时,不仅已有的厂商增加产量,而且新厂商可以进入该行业。
3.时间的长短;
可以说,这是影响供给弹性大小的最主要的因素。在极短时期内,供给量限于已有库存,无法随价格变化而变化,弹性近似为零;在短时间内,厂商能够加大可变投入(如原材料、劳动力)来扩大产量,因而弹性增大;在长期内,现有厂商可调整生产规模(包括兴建新工厂),新厂商可以进入该行业,故供给弹性变得非常大。
4.产量的大小。
从某一行业来说,在产量很小的时候,要扩大产量是很容易的,供给接近完全富于弹性;产量增加到一定程度后,生产该商品的生产要素的稀缺性开始显露出来,要进一步增加这些要素的投入(如懂行的工程师、熟练工人、特殊原料)难度加大,成本上升,从而供给弹性变小。当产量达到一定极限时,所有相关要素都己耗尽,要进一步增加产量几乎不可能了,此时,不管价格如何上涨,供给弹性几乎为零。当然,对某一种商品来说,这种极限很晚才会出现,在此之前,由于成本上升带来的价格上涨,早已把消费者的需求限制住了。
3.6 需求的经验估计
3.6.1市场调查法
即通过市场调查来获取数据,并对数据进行分析来得出结论的方法,一般包括询问、谈话、观察、问卷、实验等。其中最主要的方法是访问和实验。
3.6.2统计分析法
最主要的是回归分析法,其简单步骤为:
1.确定自变量;一种商品的需求受许多因素的影响,但是建立回归模型,一般要找出其主要的影响因素。
2.收集需求量与所选择自变量的数据;对数据要加以鉴别、整理,比如剔除那些突发事件而使需求产生异常变化的数据,或对数据加以平滑修正后再使用。
3.确定方程形式
线型模型Q=a+b1x1+b2x2+……+bnxn ;式中,x1,x2…xn为各个自变量,b1,b2,…bn为待估参数。线性模型的优点在于简单,易估计,且经验表明,许多需求函数在相当长一段时间内基本是划性关系。
指数模型Q=ax1e1x2e2…xnen(e1,e2,…en为待估计参数)。指数模型的优点:一是它反映了一个自变量对需求的边际影响并不是固定不变的,而是取决于这个自变量的值以及函数中其它所有自变量的值。此外,指数模型的优点,还在于它能容易地转变为线性函数,只要对方程两边取对数,就有:
logQ=loga+e1logx1+e2logx2+…enlogxn
它的另一特性是,需求关于各自变量的弹性恰好是各自的指数ei,是常数,与点的位置无关。
4.确定待估系数