第4章 企业生产分析

4.1生产与生产函数

4.1.1生产及生产要素
　　 企业进行生产的过程就是从生产要素的投入到产品的产出的过程。
　　 在经济学中，生产要素一般被划分为劳动、土地、资本和企业家才能这四种类型。劳动指人类在生产过程中提供的体力和脑力的总和。
　　 土地不仅指土地本身，还包括地上和地下的一切自然资源，如森林、湖泊、海洋和矿藏等。
　　 资本可以表现为实物形态或货币形态。资本的实物形态又称为资本品或投资品，如厂房、机器设备、动力燃料、原材料等。资本的货币形态通常称为货币资本。
　　 企业家才能指企业家组织建立和经营管理企业的才能。通过对生产要素的运用，企业可以提供各种实物产品，如房屋、食品、机器、日用品等，也可以提供各种无形产品即劳务，如医学、金融服务、旅游服务等。

4.1.2生产函数
　　 生产过程就是从生产要素的投入到产品的产出过程。生产过程中生产要素的投入量和产品产出量之间的关系，可以用来表示。
　　 生产函数表示在一定时期内，在技术水平不变的情况下，生产中使用的各种生产要素的数量与所能生产的最大产量之间的关系。任何生产函数都以一定时期内的生产技术水平不变作为前提条件，一旦生产技术水平发生变化，原有的生产函数就会发生变化，从而形成新的生产函数。
　　 假定L、K、N、E表示产品生产过程中使用的劳动、资本、土地和企业家才能等生产要素的投入量，Q表示所能生产的最大产量，则生产函数可以写成以下形式: Q = f ( L, K, N, E )
　　该生产函数表示在既定的生产技术水平下生产要素组合(L、K、N、E)在每一时期所能生产的最大产量为Q。
　　 在经济学的分析中，为了简化分析，通常假定生产中只使用劳动和资本这两种生产要素。若以L表示劳动投入量，以K表示资本投入量，则生产函数简写为: Q = f ( L, K )
　　 生产函数表示生产中投入量和产出量之间的依存关系，这种关系普遍存在于各种生产过程之中。

4.1.3柯布－道格拉斯生产函数
　　 20 世纪30年代，美国经济学家柯布(Charbes W.Cobb)和道格拉斯(Paul H.Dorglas)根据1599－l922年美国的资本和劳动这两种生产要素的投入和产出的关系，得出这一期间的美国制造业的生产函数，以后扩大应用于整个经济或任何一个生产领域。该生产函数的一般形式为：
　　 Q = A L ^α K ^β
　　 式中，Q为产量；L和K分别为劳动和资本投入量；A，α，β为三个参数，0< α， β< 1。柯布－道格拉斯生产函数中的参数α和β的经济含义是:当α+β=l时，α和β分别表示劳动和资本在生产过程中的相对重要性，α为劳动所得在总产量中所占的份额，β为资本所得在总产量中所占的份额。
　　 根据柯布和道格拉斯对美国1599－1922年期间有关经济资料的分析和估算，α值约为0.75，β值约为0.25。它说明，在这一期间的总产量中，劳动所得的相对份额为75%，资本所得的相对份额为25%。

4.1.4技术系数
　　 生产不同的产品时，企业所投入的各种生产要素的配合比例是不同的，为生产一定数量的某种产品所需要的各种生产要素的配合比例称为技术系数。
　　 4.1.5短期与长期的经济学界定
　　 微观经济学中的短期生产是指生产者不能随产量的变化而调整全部生产要素的数量的时间周期，即至少有一种生产要素的数量是固定不变的时间周期。长期生产是指生产者可以随产量的变化调整全部生产要素数量的时间周期。相应地，在短期内，生产要素投入可以分为不变投入和可变投入，生产者在短期内不能进行数量调整的那部分要素投入是不变投入要素，例如，机器设备、厂房等。生产者在短期内可以进行数量调整的那部分要素投入是可变投入要素，例如，劳动、原材料、燃料等。在长期内生产者可以随产量的变化调整全部的要素投入。例如，生产者可以扩大或缩小生产规模，甚至还可以进入或退出一个行业的生产。由于在长期内所有的要素投入量都是可变的，因而也就不存在可变投入要素和不变投入要素的区分。
　　 在这里，短期和长期的划分依据是以生产要素能否随产量的变化而调整作为标准的。对于不同的行业，短期和长期的界定是不同的。比如：变动一个大型汽车制造厂的规模可能需要三年的时间，而变动一个快餐店的规模可能只需要一个月时间，即前者的短期生产与长期生产的划分为三年，而后者仅为一个月。

4.2一种可变要素的生产函数

4.2.1生产函数
　　 假设只有一种投入要素的是可变的，其它投入要素是固定不变的。该生产函数是一种短期生产函数。如果用K表示固定要素的资本投入量，用L表示可变要素的劳动投入量，则生产函数可以写成:Q=f(L，K)，即一种可变生产要素的生产函数的形式，它也被称为短期生产函数。

4.2.2总产量、平均产量和边际产量
　　 1.总产量、平均产量和边际产量
　　 短期生产函数Q=f(L，K)表示在资本投入量固定时，由劳动投入量变化所带来的最大产量变化。由此，可以得到劳动的总产量(Total Product)，劳动的平均产量(Average Product)和劳动的边际产量(Marginal Product)这三个概念。总产量、平均产量和边际产量的英文简写分别是TP_L，AP_L，和MP_L。
　　 劳动的总产量TP_L是指固定投入要素资本与一定的可变投入要素劳动相结合所能生产的最大产量。其定义 TP_L=f ( L, K )
　　 劳动的平均产量AP_L是指总产量与所使用的可变投入要素劳动之比。其定义为：
　　 劳动的边际产量MP_L是增加一单位可变投入要素劳动所增加的产量。其定义为：
　　 如果固定投入要素是劳动，可变投入要素是资本，对于生产函数Q=f(L，K)来说是在劳动投入量固定时，由资本投入量所带来的最大产量的变化。由此生产函数可以得到相应的资本的总产量，资本的平均产量和资本的边际产量，它的定义公式分别为:

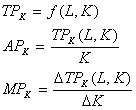
　　 以某企业一种可变生产要素的生产函数为例，可以得到总产量，平均产量和边际产量的变化趋势。如表4.1所示。

表 4-1 总产量、平均产量和边际产量

2.总产量曲线、平均产量曲线和边际产量曲线
　　 根据表4-1的数值可以画出总产量，平均产量和边际产量的曲线如图4-1所示。

图中的横轴表示可变要素劳动的投入数量L，纵轴表示产量Q，TP_L为总产量曲线，AP_L为平均产量曲线，MP_L为边际产量曲线。从图中可以知道，随着劳动投入量的增加，开始时总产量，平均产量和边际产量都是先呈上升趋势，而达到各自最大值之后，再呈下降趋势。

4.2.3边际收益递减规律
　　 由表4-1和图4-1可以清楚地看到，对一种可变生产要素的生产函数来说，边际产量表现出先上升而最终下降的特征，这一特征被称为边际收益递减规律。
　　 所谓边际收益递减规律是指在技术水平不变的条件下，在固定的投入要素上连续等量追加一种可变生产要素，总产量、平均产量和边际产量先上升而后呈递减的趋势。 边际收益递减规律是短期生产的一条基本规律，这一规律发生作用的前提是技术水平不变，技术水平不变是指生产中所使用的技术没有发生重大变革。现在，技术进步的速度很快，但并不是每时都有重大的技术突破，技术进步总是间歇式进行的，只有经过一定时期的准备以后，才会有重大的进展。无论是在农业中还是在工业中，一种技术水平一旦形成，总会有个相对稳定的时期，这一时期就可以称为技术水平不变。离开了技术水平不变这一前提，则边际收益递减规律就不能成立。
　　 边际收益递减规律强调的是，在任何一种产品的短期生产中，随着一种可变要素投入量的增加，边际产量最终必然呈出现递减的特征。边际收益递减规律成立的原因是短期生产中，生产要素之间存在最佳配合比例关系。

4.2.4总产量、平均产量和边际产量相互之间的关系
　　
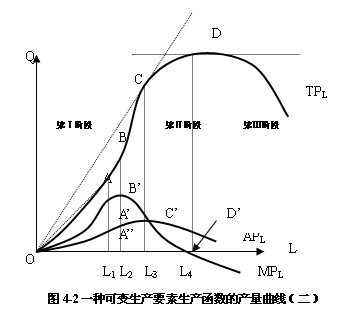
　　 总产量、平均产量和边际产量的相互关系如图4-2所示，一种可变生产要素的生产函数的产量曲线图，它反映了短期生产的有关产量曲线相互之间的关系。
　　 在图4-2中可以清楚地看到，由边际收益递减规律决定的劳动边际产量MP_L曲线，先是上升的，并在B′点时达到最高点，然后再下降。由短期生产的这一基本特征出发，我们利用图4-2，从以下三个方面分析总产量、平均产量和边际产量一种可变生产要素的生产函数相互之间的关系。
　　 第一，边际产量和总产量之间的关系。
　　 根据边际产量的定义公式:
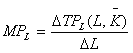
　　 可知，过TPL，线上任何一点的切线的斜率就是相应的MP_L值。例如，在图中，当劳动投入量为L1 时，过TP_L曲线上A点的切线的斜率，就是相应的MP_L的值，它等于L1的高度。
　　 正是由于每一个劳动投入量上的边际产量MP_L值就是相应的总产量TP_L曲线的斜率，所以，在图中MP_L曲线和TP_L 曲线之间存在这样的对应关系:在劳动者投入量小于L4的区域，MP_L均为正值，则相应的TP_L线的斜率为正，即TP_L曲线是上升的；在劳动投入量大于L4的区域， MP_L均为负值，则相应的TP_L线的斜率为负，即TP_L曲线是下降的。当劳动投入量恰好为L4时，MP_L为零值，则相应的TP_L曲线的斜率为零，即TP_L曲线达到极大值点。也就是说MP_L曲线的零值点D,和TP_L最大值点D是相互对应的。以上这种关系可以简单表述为:只要边际产量是正的，总产量总是增加的，只要边际产量是负的，总产量总是减少的，当边际产量为0时，总产量达到最大值点。
　　 第二，平均产量和总产量之间的关系。
　　 根据平均产量的定义公式 ：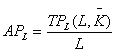
　　 可知，连接TP_L曲线上任何一点和坐标原点的线段斜率，就是相应的AP_L值，例如在图中，当劳动投入量为L1时连接TP_L曲线上A点和坐标原点的线段OA的斜率即就是相应的AP_L值。
　　 正是由于这种关系，所以，在图中当AP_L曲线在C′点达最大值时TP_L曲线必然有一条从原点出发的最陡的切线。其切点为C点。
　　 第三，边际产量和平均产量之间的关系。
　　 在图中，我们可以看到MP_L曲线和AP_L曲线之间存在着这样的关系:两条曲线相交于AP_L曲线的最高点C′。在C′点之前，MP_L曲线高于AP_L曲线，在C′,点之后，MP_L曲线低于AP_L曲线，不管是上升还是下降，MP_L曲线的变动都快于AP_L曲线的变动。
　　 就任何一对边际量和平均量而言，当MP_L>AP_L时，AP_L曲线是上升的，当MP_L< AP_L时，AP_L曲线是下降的。又由于边际报酬递减规律作用下的MP_L曲线是先升后降的，所以，当MP_L曲线和AP_L曲线相交时，AP_L曲线必达最大值。
　　 此外，由于在可变以要素劳动投入量的变化过程中，边际产量的变动相对于平均产量的变动而言要更敏感一些，所以，不管是增加还是减少，边际产量的变动都快于平均产量的变动。

4.2.5生产要素的合理投入
　　 为了确定劳动这种可变生产要素的合理投入，可根据图4-2的总产量曲线、平均产量曲线和边际产量的变化把生产分为三个阶段：
　　 第一阶段是劳动投入量从0增加到L₃(图4-2的Ⅰ)，平均产量达到最大值。
　　 在这一阶段产量曲线特征为:劳动的平均产量始终是上升的，且达到最大值，劳动的边际产量上升达到最大值，且劳动的边际产量始终大于劳动的平均产量；劳动的总产量始终是增加的。说明在这一阶段，不变要素资本的投入量相对过多，生产者增加可变要素劳动的投入量是有利的，或者说，生产者只要增加可变要素劳动的投入量，就可以增加总产量。因此，任何理性的生产者都不会在这一阶段停止生产，而是连续增加可变要素投入量以增加总产量并将生产扩大到第二阶段。
　　 第二阶段是劳动投入量从L₃增加到L₄(图4-2的Ⅱ)平均产量开始下降，但边际产量仍然大于零，总产量仍在增加。
　　 第三阶段是劳动量增加到L₄以后(图4-2中Ⅲ)，劳动的平均产量继续下降，劳动的边际产量降为负值，劳动的总产量也呈现下降的趋势。
　　 这说明在这一阶段，可变要素劳动的投入量相对过多，生产者减少可变要素劳动的投入量是有利的，因此，这时即使劳动要素是充足供给的，理性的生产者，也会通过减少劳动投入量来增加总产量，以摆脱劳动的边际产量为负值和总产值下降的局面，并退回到第二阶段。由此可见，任何理性的生产者不会将生产停留在第一阶段，也不会将生产扩张到第三阶段，所以，生产只能在第二阶段进行。在生产的第二阶段，生产者可以得到由于第一阶段增加可变要素投入所带来的全部好处，又可以避免将可变要素投入增加到第三阶段而带来不利的影响。因此，第二阶段是生产者进行短期生产的合理投入区间。在第二阶段的起点处，劳动的平均产量曲线和劳动者的边际产量曲线相交，即劳动者的平均产量达到最高点。在第二阶段的终点处，劳动的边际产量曲线与水平轴相交即劳动的边际产量等于零。至于在生产的第二阶段，生产者所应选择的劳动投入数量究竟在哪一点，这一问题还有待于以后结合成本、收益和利润进行深入的分析。

4.3两种可变生产要素的生产函数

4.3.1生产函数
　　 在长期内，所有的生产要素的投入量都是可变的，多种可变生产要素的长期生产函数可写为：Q= f ( L, K, N, E )
　　 式中Q为产量，L、K、N、E分别表示产品生产过程中使用的劳动、资本、土地和企业家才能等生产要素的投入量。该生产函数表示长期内，在技术水平不变的条件下，由几种可变生产要素投入量的一定组合所能生产的最大量。
　　 在生产理论中，为了使分析简化，通常以两种可变生产要素的生产函数来考察长期生产问题。假定生产使用劳动和资本两种可变生产要素生产一种产品，则两种可变生产要素的长期生产函数可以写为: Q = f ( L, K )
　　 式中，L为可变要素劳动的投入量；K为可变要素资本的投入量，Q为产量。

4.3.2等产量曲线
　　 生产理论中的等产量曲线和效用理论中的无差异曲线是很相似的。等产量曲线是在技术水平不变的条件下生产同一产量的两种生产要素投入量的所有不同组合的点的轨迹。

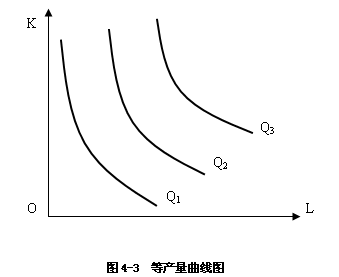
同一平面上可以有许多条等产量曲线。每一条曲线代表生产一定产量的劳动和资本的所有可能的不同组合。
　　 与无差异曲线相似，等产量曲线与坐标原点的距离的大小表示产量水平的高低；离原点越远的等产量曲线代表的产量水平越高。同一平面坐标上任意两条等产量曲线不会相交。
　　 图4-4表明两种要素替代程度不同，它们的等产量曲线的形状也不同。
　　 图4-4（a）表示如果两种生产要素是完全替代品，等产量线将是一条直线；
　　 图4-4（b）表示如果两种生产要素替代不完全，等产量曲线就稍有弯曲；
　　 图4-4（c）表示如果两种生产要素只能以一个固定的比例进行生产，换言之，生产要素完全无法替代，那么等产量线就成折线。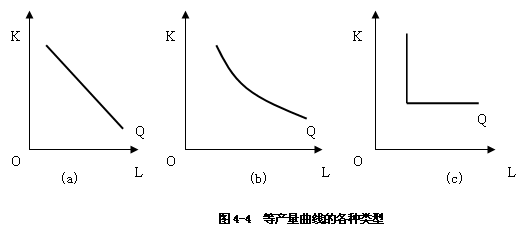

4.3.3边际技术替代率递减规律
　　 1.边际技术替代率
　　 等产量曲线表示一个既定的产量水平可以由两种可变要素的各种不同数量的组合。这就意味着，生产者可以通过两要素之间的相互替代，来维持一个既定的产量水平，例如:为了生产固定单位的某种产品，生产者可以使用较多的劳动和较少的资本，也可以使用较少的劳动和较多的资本。前者可以看成是劳动对资本的替代，后者可以看成资本对劳动的替代。由两种要素之间这种相互替代的关系，可以用边际技术替代率来表示。在维持产量水平不变的条件下，增加一单位某种生产要素投入量与所减少的另一种生产要素的投入量的比率，被称为边际技术替代率。边际技术替代率的英文缩写为MRTS。劳动对资本的边际技术替代率的定义公式为：
　　 式中△K和△L，分别为资本投入量的变化量和劳动投入量的变化量。公式中加一负号是为了使MRTS值在一般情况下为正值，以便于比较。△L→0，则相应的边际技术替代率公式为：
　　 显然等产量曲线上某一点的边际技术替代率就是等产量曲线在该点斜率的绝对值。
　　 假定资本和劳动的边际产量分别为MP_K和MP_L，那么，减少资本投入所减少的产量等于△K×MPK；增加劳动投入，所增加的产量等于△L×MP_L。
　　 两者相等即为△K×MP_K =△L×MP_L也就是△K/△L =MP_L/MP_K。
　　 因此，MRTS_LK=-△K/△L=MP_L/MP_K。可见，边际技术替代率可以表示为两要素边际产量之比。

2.边际技术替代率递减规律
　　 在两种生产要素相互替代的过程中，普遍地存在这种现象，即在维持产量不变的前提下，当一种生产要素的投入量不断增加时，每一单位的这种生产要素所能替代的另一种生产要素的数量是递减的。这一现象被称之为边际技术替代率递减规律。
　　 边际技术替代率递减的主要原因在于，任何一种产品的生产技术要求各要素投入之间的适当比例，这意味着要素之间替代是有限的。简单地说，以劳动和资本两种要素投入为例，在劳动投入量很少和资本投入量很多的情况下，减少一些资本投入量可以很容易通过增加劳动投入量来弥补，以维持原有的产量水平，即劳动对资本的替代很容易。但是在劳动投入增加到相当多的数量和资本投入量减少到相当少的情况下，再用劳动去替代资本，那将是很困难的了。

4.3.4等成本线
　　 等成本线是指在一定时期内，在既定的成本和既定的生产要素价格条件下，企业可以购买到两种生产要素所有可能的组合。假定要素市场上既定的劳动价格即工资率为W，既定资本价格即利息率为r，企业既定的成本支出为C，则成本方程为：
　　 根据以上公式可以得等成本线，如图4-5所示。由于上式中成本方程式是线性的,所以等成本线是一条直线。
　　 在图4-5中等成本线以内区域中的任何一点，如A点，表示即定的全部成本都用来购买该点的劳动和资本的组合后还有剩余。等成本线外的区域中的任何一点，如B点表示用既定的全部成本购买该点的劳动和资本组合是不够的，唯有等成本线上的任何一点。才表示用既定的全部成本能刚好购买到的劳动和资本的组合。
　　 在成本和生产要素价格既定条件下，便可以得到一条等成本线，任何关于成本和要素价格的变化，都会使等成本线发生变化。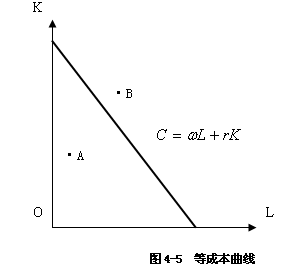

4.3.5生产要素的最优组合
　　 生产要素的最优组合(Optimum Factor Combination)，是指以最小成本生产最大产量的生产要素的配合比例，又称之为生产者均衡，因为实现了要素的最优组合，也就是达到了利润最大化，如果其他条件不变，生产者就不愿意再改变两种生产要素的配合比例。在图形上，生产要素的最优组合是等产量曲线和等成本线的相切之点。具体说，有两种情况：
　　 1.产量既定条件下最小成本的生产要素组合。
　　 如图4-6所示，由于产量既定，所以只有一条等产量曲线。图中有3条等成本线，C₁的成本水平太低，不能生产产量水平Q。生产同样的产量，企业既可以选择C₃的两个交点M和N所对应的两种生产要素的组合,也可以选择C₂代表的成本水平，使用等产量曲线和C₂的切点E所对应的两种要素的组合。很显然，只有E点所代表的劳动与资本的组合，才是企业的生产均衡点。
　　 2.成本既定条件下的最大产量的生产要素组合。
　　 如图4-7所示，由于成本既定，所以图中只有一条等成本线.但有三条等产量曲线。其中Q₃代表的产量水平最高，但既定的总成本太低，无法生产Q₃代表的产量水平。等成本线与Q₁也有两个交点M和N，与Q₂有一个切点E，这说明既定的成本支出既可以采取M和N所代表的要素组合生产Q₁的产量，也可以采取E点所代表的要素组合生产Q₂的产量。由于Q₂代表的产量水平大于Q₁，所以只有E点才是生产要素的最优组合之点。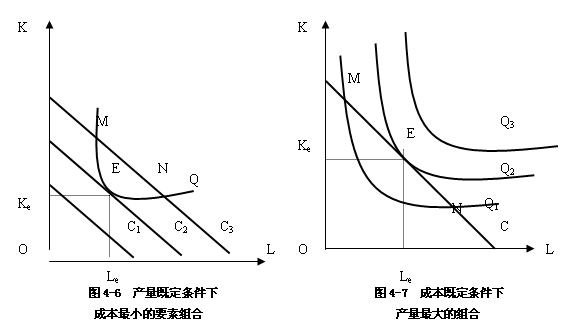
　　 无论是产量既定，还是成本既定，等成本线和等产量线的切点E，都是生产者的均衡点。在该点上，等产量曲线的斜率正好等于等成本线的斜率。由于等产量曲线的斜率的经济含义是两种生产要素的边际产量之比，而等成本线斜率的经济含义是两种生产要素的价格之比，所以.生产者均衡或要素最优组合的条件是:

　　 该式的经济含义是，如果劳动和资本两种生产要素可以完全替代，那么使用这两种要素的配合比例不仅要视它们各自的边际产量，而且要视它们各自的价格而定。企业可以通过对两要素投入量的不断调整，使每一元成本无论用来购买哪一种生产要素所获得的边际产量都相等，从而实现生产要素的最优组合。

4.3.6脊线与生产扩展线
　　 1.生产的经济区域
　　 图4-5中，就其中任一条等产量曲线而言，并非在曲线每一点的斜率都是负值，也就是说并非曲线上每一点边际技术替代率都是正的值。
　　 在每一条等产量线上，都有这样的点，劳动L的边际产量等于0，该处的劳动L对资本K的边际技术替代率等于0，等产量线的切线斜率等于0，如图中的A1、A2、A3点等。连接所有这样的点，构成OA线。在OA线上，劳动的边际产量等于0，这时如果继续增加劳动的投入，而资本的投入保持不变，劳动的边际产量会变为负，总产量不仅不会上升，反而会下降。
　　 同样，在每一条等产量线上，也都有这样的点，资本K的边际产量等于0，该处的劳动L对资本K的边际技术替代率等于∞，等产量线切线斜率为∞，如图中的B1、B2、B3点等，连接所有这样的点，构成OB线。在OB线上，资本的边际产量等于0，这时如果继续增加资本的投入，而劳动的投入保持不变，资本的边际产量也要变为负，从而引起总产量的下降。

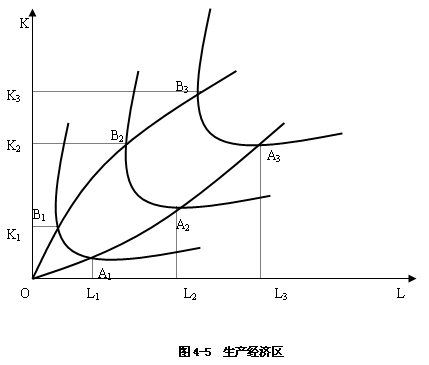
由此可知，OA线构成了使用劳动数量的上限，在OA线右边的点，劳动的边际产量为负；OB线构成了使用资本的上限，在OB线的左边的点，资本的边际产量为负。OA，OB所围成的区域叫生产经济区，OA、OB两条线叫脊线，所谓脊线是指连接等产量曲线上边际技术替代率为零与连接等产量曲线上边际技术替代率为无穷大的线。脊线以内区域为生产的经济区域，脊线以外的区域为生产的非经济区域。理性的生产者将生产应选择在生产的经济区域，这样做不至于造成资源的浪费。由图4-5可以看出，在脊线以外的区域，等产量曲线的斜率是正的值。这表明，在脊线以外的区域，为了维持既定的产量水平，在增加一种要素的同时必须增加另一种要素，要素之间并不存在替代的关系。若将生产从脊线以外的区域移到脊线以内的区域既维持既定产量水平，又节约了资本与劳动两种要素的投入量，在这区域，劳动与资本两种要素存在着互替代关系，因此，脊线以内的区域是生产的经济区域。

2.生产扩展线
　　 在生产要素的价格、生产技术和其他条件不变时，如果企业改变成本，等成本线就会发生平移；如果企业改变产量，等产量曲线也会发生平移，这些不同的等产量曲线将与不同的等成本线相切。形成一系列不同的生产均衡点，这些生产均衡点的轨迹就是扩展线（Productive Expasion Curve）。
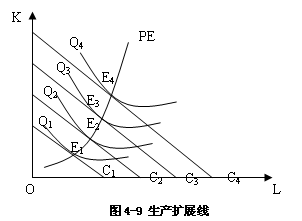
　　 生产扩展线是在生产要素价格不变的情况下企业扩大生产规模所引起的生产要素最优组合点变动的轨迹。在生产扩展线上，可以用最小成本生产最大产量，从而获得最大利润，所以企业愿意沿此路径扩大生产。但企业究竟会把生产推进到扩展线的哪一点上，单凭扩展线是不能确定的，还要看市场上的需求情况。

4.4 规模报酬

4.4.1规模报酬的类型
　　 规模报酬分析涉及的是企业的生产规模变化与所引起的产量变化之间的关系。企业只有长期内才有可能变动全部生产要素，进而变动生产规模，因此，企业的规模报酬分析属于长期生产问题。
　　 在生产理论中，通常是全部的生产要素都以相同的比例发生变化来定义企业的生产规模的变化。相应地，规模报酬变化是指在其他条件不变的情况下，企业内部各种生产要素按相同比例变化时所带来的产量变化。企业的规模报酬变化可以分规模报酬递增、规模报酬不变和规模报酬递减三种情况。
　　 1.规模报酬递增(Increasing Returns to Scale)，是指产量增加的比例超过了要素投入量增加的比例。
　　 对于规模报酬递增的生产函数来讲，劳动与资本扩大一个很小的倍数就可以导致产出扩大很大的倍数。如图4-10，当劳动与资本分别投入为2个单位时，产出为100个单位，但是生产200单位的产量所需要的劳动与资本的投入分别少于4个单位。产出是原来的2倍，投入却不到原来的2倍。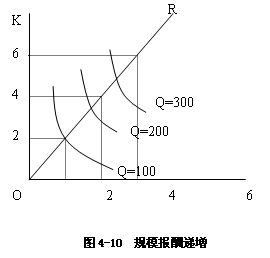
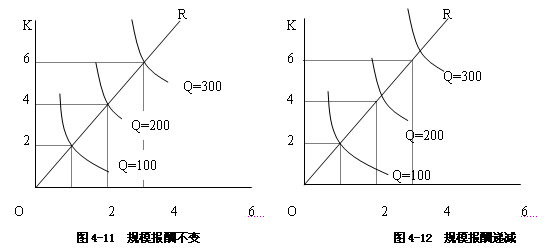
　　 2.规模报酬不变（Constant Returns to Scale），指各种要素的投入量增加的比例和产量增加的比例相同。
　　 如图4-11所示，对于规模报酬不变生产函数来讲，投入量扩大某一倍数，产出也扩大相应的倍数。当劳动与资本投入分别为4个单位时，产出为200个单位，产出与投入扩大了相同的倍数。

3.规模报酬递减(Decreasing Returns to Scale)，是指产量增长的比例小于要素投入量增加的比例。
　　 如图4-12所示，对于规模报酬递减的生产函数来讲，劳动与资本来扩大一个很大的倍数只能导致产出扩大很小的倍数。当劳动与资本分别投入2个单位时产出为100单位，但是当劳动与资本分别投入为4个单位时产出水平低于200个单位。投入量是原来的2倍。但产出增加却不及原来的2倍。

4.4.2规模报酬的判断
　　 令生产函数Q=f(L，K)。
　　 如果 ，其中，常数λ>0，则生产函数Q=f(L，K)具有规模报酬递增的性质。
　　如果 ，其中，常数λ>0，则生产函数Q=f(L，K)具有规模报酬不变的性质。
　　 如果 ，其中，常数λ>0，则生产函数Q=f(L，K)具有规模报酬递减的性质。
　　 一般说来，在长期生产过程中，企业的规模报酬的变化呈现出如下的规律:当企业从最初的很小的生产规模开始逐步扩大的时候，企业面临的是规模报酬递增的阶段。在企业得到了由生产规模扩大所带来的产量递增的全部好处以后，一般会继续扩大生产规模，将生产保持在规模报酬不变的阶段。这个阶段有可能比较长。在这以后，企业若继续扩大生产规模，就会进入一个规模报酬递减的阶段。

4.4.3影响规模报酬的因素
　　 1.引起规模报酬递增的因素
　　 第一，可以使用更加先进的机器设备。
　　 当生产规模较小时，无法购买先进的大型设备，即使购买了也无法充分发挥效用，只有在大规模生产中，大型的先进设备才能充分发挥其作用，使产量更大幅度地增加；
　　 第二，可以进行专业化分工。
　　 在大规模的生产中，专业可以分得更细，分工更细，这样有利于提高生产效率；
　　 第三，生产要素的不可分割性；
　　 生产规模的扩大使企业有可能利用先进的生产设备，而大批量生产的设备通常是不可分割的，如彩电生产流水线、汽车生产流水线，若将它们分割，无法发挥其技术上的优势。；
　　 第四，几何尺度的因素；
　　 大设备单位能力的制造和运转费用通常比小设备低。
　　 第五，可以对副产品进行综合利用；
　　 在小规模生产中，大多副产品往往被作为废物处理，而在大规模生产中，就可以对这些副产品进行再加工，做到“变废为宝”。
　　 第六，财务方面的因素；
　　 企业活动的大规模化会给它带来筹措资金，购买原材料、半成品及销售等方面的好处此外，在生产要素的购买与产品的销售方面也会更加有利。
　　 其他因素，生产规模扩大后，管理、行政费用一般会等比例增加，而分摊到每一位单位产品的平均管理费用有所降低，等等。

2.引起规模报酬递减的因素
　　 第一，管理效率的降低；
　　 规模扩大带来管理层次增多，部门间的横向、纵向沟通就更为困难，管理上出现各种漏洞，从而使产量和收益反而减少。
　　 第二，生产要素价格与销售费用增加，生产要素的供给并不是无限的，生产规模过大，必然大幅度增加对生产要素的需求，从而使生产要素的价格上升。同时，生产规模过大，产品大量增加，也增加了销售困难，需要增设更多的销售机构和人员，从而增加了销售费用。
　　 此外，从规模扩大中能获得的经济利益有限，它受到技术和管理上的限制，不同工业部门的规模经济性也存在较大差异。同时生产要素的分工也有限度，无限止的细分，将带来副作用。比如，工人会失去创造性思维，得不到工作中的学习、激励、创造的乐趣，会降低劳动生产率，等等。因此，生产规模并非越大越好。

4.5 技术进步

4.5.1技术进步的概念
　　 技术进步是指在创造和掌握新知识的基础上，进一步在生产领域的各个阶段和非生产领域应用新知识的过程。技术进步对经济发展的直接作用是:在相同费用下生产的产品更好，或者在同一产品上花的费用更低。技术进步通过两种形式交替作用而完成，一种是技术革命，即由于重大的变革和创造而引起的技术发展的飞跃性质变；另一种是技术革新，即在技术上渐进性的量的进步。在当今社会，由于新技术在若干重要领域内的突破，使得飞跃性质变的技术发展成为当代技术进步的基本内容和核心。
　　 技术进步的重要意义在于社会经济发展在不增加资金和劳动力的条件下，通过内涵扩大再生产来实现。其主要标志是：（1）提高技术装备水平；（2）改革工艺，采用新材料；（3）提高劳动者素质；（4）提高管理决策水平；（5）社会生产力得到迅速发展；（6）社会生产关系和社会生活发生变化，等等。
　　 技术进步使得较少的投入就能够生产出和以前同样多的产品。所以，技术的进步导致了生产函数的变化，这种变化可以用等产量线的位移来说明。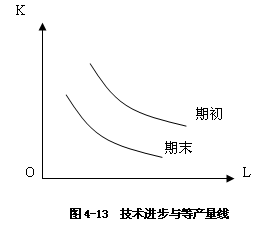
　　 如图4-13所示，图中的两条等产量线代表的产量都是Q0，一为期初，一为期末。期末的等产量线表明，用比期初少的资本和劳动的投入就可以生产出与期初同样多的产品，这说明在这期间技术进步了。用等产量线的位移程度来说明技术进步的程度，位移越大，说明技术进步越快。

4.5.2技术进步的类型
　　 技术进步的结果还往往会导致生产过程中投入要素的优化选择点发生变动，投入要素的比例发生变动。为了便于比较，假定在技术变动前后投入要素价格相对不变，而且在产量相同的条件下进行。技术进步必然要引起投入要素的边际产量的变动，而不同要素边际产量变动的比例不一定相同。在可变投入是资本和劳动的情况下，根据资本边际产量和劳动边际产量变动的不同将技术进步分为劳动节约型技术进步，资本节约型技术进步和中性型技术进步。
　　 1． 劳动节约型技术进步
　　 在劳动节约型技术进步中，技术进步的结果是使资本边际产量的变化大于劳动边际产量的变化，资本的边际产量提高得更快。在资本和劳动的价格比保持不变的情况下，原来的生产者优化选择点不合适了，应当增加资本的投入，减少劳动的投入，使资本的边际产量有所下降，劳动的边际产量有所提高，直到资本的边际产量和劳动的边际产量之间的比再次等于资本和劳动的价格比时，生产者再次达到优化选择点。如图4-14所示，优化选择点从E0移至E1，这时投入资本和劳动之间的数量比例就改变了，必然是资本占的比重增加，劳动占的比重减少。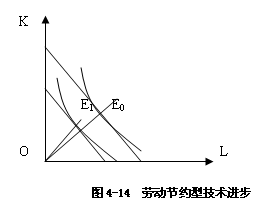
　　 2．资本节约型技术进步
　　 在资本节约型技术进步中，技术进步的结果使劳动的边际产量的变化大于资本边际产量的变化，要增加劳动的投入，减少资本的投入，直到劳动的边际产量和资本的边际产量之间的比再次等于劳动与资本的价格比时，生产者也就达到了新的优化选择点，如图4-15所示，优化选择点从E0移到E1，不过这次是劳动所占的比重增加，资本所占的比重减少。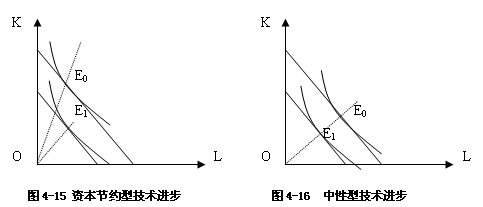

3.中性型技术进步
　　 在中性型技术进步中，技术进步的结果是资本和劳动的边际产量的变化相同。虽然资本边际产量与劳动边际产量之比仍保持资本与劳动的价格之比，但是由于边际产量的数值已经提高了，要维持原有的产量，投入的资本和劳动的数量都要减少，且减少的比例相同，使各自在总投入中的比重保持不变。如图4-16所示，选择从E0移到E1，这称作中性型技术进步。

4.5.3.技术进步对经济发展的推动作用
　　 具体地讲，技术进步对经济发展的推动作用主要体现在以下几个方面：
　　 1.技术进步可以减少对自然资源的依赖，提高经济发展的稳定性，增强国民经济在国际市场上的竞争能力。经济发展往往受到本国自然资源的约束，而因此依赖于国际市场，一旦自然资源减少，或国际市场价格上涨时，常使经济发展遭受重大挫折。技术进步推动新产品开发，随着新能源、新材料的发现和应用，以及降低消耗、节约投入，必然使本国经济持续稳定地发展。
　　 2.自动化、机械化逐步代替人力，使劳动生产率大幅度提高，而且自动化和机械化的日益进步，也使资本收益率越来越高。
　　 3.技术进步使劳动者的素质不断提高，劳动者能够掌握越来越复杂的技术、工程知识，操作能力不断提高。
　　 4.技术进步使工艺、产品质量提高，产品的花色品种不断增加，丰富了人们的生活内容，改善了消费质量和消费结构，有利于提高劳动者的积极性。
　　 5.在原材料和能源等方面的技术创新，一方面使能源和原材料消耗减少，另一方面大大提高了其使用效率，从而使生产的投入越来越节约，而产出水平越来越提高，为经济效益的提高奠定了基础。
　　 6.技术进步改变了人们的文化观念、工作方式、生活方式、组织形式和管理方式，使人们的思想观念现代化，给经济增长的内容创造了新的社会形式。
　　 概而言之，技术进步可以使技术功效增大，即技术变动后用同样的投入可以生产更多的产品，或者是生产同样数量的产品，只用较少的投入。