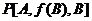您的当前位置是：第二章 知识表示方法>>学习内容>>知识点三

观看视频讲解，学习谓词逻辑法

一、谓词演算

1．语法和语义

谓词逻辑的基本组成部分是谓词符号、变量符号、函数符号和常量符号，并用圆括弧、方括弧、花括弧和逗号隔开，以表示论域内的关系。

原子公式是由若干谓词符号和项组成，只有当其对应的语句在定义域内为真时，才具有值T（真）；而当其对应的语句在定义域内为假时，该原子公式才具有值F（假）。

2．连词和量词

连词有∧（与）、∨（或），全称量词（x），存在量词（x）。

原子公式是谓词演算的基本积木块，运用连词能够组合多个原子公式以构成比较复杂的合适公式。

3．几个有关定义

用连词∧把几个公式连接起来而构成的公式叫做合取，而此合取式的每个组成部分叫做合取项。一些合适公式所构成的任一合取也是一个合适公式。

用连词∨把几个公式连接起来所构成的公式叫做析取，而此析取式的每一组成部分叫做析取项。由一些合适公式所构成的任一析取也是一个合适公式。

用连词→连接两个公式所构成的公式叫做蕴涵。蕴涵的左式叫做前项，右式叫做后项。如果前项和后项都是合适公式，那么蕴涵也是合适公式。

前面具有符号～的公式叫做否定。一个合适公式的否定也是合适公式。

量化一个合适公式中的某个变量所得到的表达式也是合适公式。如果一个合适公式中某个变量是经过量化的，就把这个变量叫做约束变量，否则就叫它为自由变量。在合适公式中，感兴趣的主要是所有变量都是受约束的。这样的合适公式叫做句子。

二、谓词公式

1．谓词合适公式的定义

在谓词演算中合适公式的递归定义如下：

① 原子谓词公式是合适公式。

② 若A为合适公式，则～A也是一个合适公式。

③ 若A和B都是合适公式，则（A∧B），（A∨B），（A=>B）和（A←→B）也都是合适公式。

④ 若A是合适公式，x为A中的自由变元，则（x）A和（x）A都是合适公式。

⑤ 只有按上述规则①至④求得的那些公式，才是合适公式。

举例：试把下列命题表示为谓词公式：任何整数或者为正或者为负。

解 把上述命题意译如下：

对于所有的x，如果x是整数，则x或者为正数或者为负数。

用I（x）表示“x是整数”，P（x）表示“x是正数”，N（x）表示“x是负数”。于是，可以把给定命题用下列谓词公式来表示：

2．合适公式的性质

① 否定之否定

～（～P）等价于P

② P∨Q等价于～P→Q

③ 狄•摩根定律

～（P∨Q）等价于～P∧～Q

～（P∧Q）等价于～P∨～Q

④ 分配律

P∧（Q∨R）等价于（P∧Q）∨（P∧R）

P∨（Q∧R）等价于（P∨Q）∧（P∨R）

⑤ 交换律

P∧Q等价于Q∧P

P∨Q等价于Q∨P

⑥ 结合律

（P∧Q）∧R等价于P∧（Q∧R）

（P∨Q）∨R等价于P∨（Q∨R）

⑦ 逆否律

P→Q等价于～Q→～P

此外，还可建立下列等价关系：

⑧ ～（x）P（x）等价于（x）［～P（x）］

～（x）P（x）等价于（x）［～P（x）］

⑨ （x）［P（x）∧Q（x）］等价于

（x）P（x）∧（x）Q（x）

（x）［P（x）∨Q（x）］等价于

（x）P（x）∨（x）Q（x）

⑩ （x）P（x）等价于（y）P（y）

（x）P（x）等价于（y）P（y）

三、置换与合一

1．置换

假元推理，就是由合适公式W₁和W₁→W₂产生合适公式W₂的运算。

全称化推理，是由合适公式（x）W（x）产生合适公式W（A），其中A为任意常量符号。

一个表达式的项可以是变量符号、常量符号或者函数表达式。函数表达式由函数符号和项组成。一个表达式的置换就是在该表达式中用置换项置换变量。

举例：表达式P［x，f（y），B］的一个置换为s1=｛z/x，w/y｝，则：P［x，f（y），B］s1=P［z，f（w），B］

2．合一

寻找项对变量的置换，以使两表达式一致，叫做合一（unification）。如果一个置换s作用于表达式集｛E_i｝的每个元素，则用｛E_i｝s来表示置换例的集。称表达式集｛E_i｝是可合一的。如果存在一个置换s使得：E_1s=E_2s=E_3s=…那么称此s为｛E_i｝的合一者，因为s的作用是使集合｛E_i｝成为单一形式。

例：表达式集的一个合一者为：

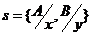
因为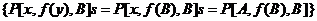

即S使表达式变成单一形式：