您的当前位置是：第三章 确定性推理>>学习内容>>知识点一

一、图搜索算法中的几个相关问题

1．搜索

图搜索是指在状态图中寻找目标或路径的搜索。所谓搜索，顾名思义，就是从初始节点出发，沿着与之相连的边试探地前进，寻找目标节点的过程（也可以反向进行）。解是由初始状态到目标状态的路径，其过程如图3.1所示。

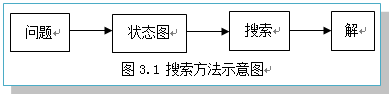
2．算法中的数据结构和符号约定

①OPEN表:记录刚刚生成的节点。

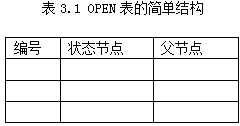
OPEN表是一种动态数据结构，专门登记当前待考查（待访问）的节点，也叫未扩展节点表。OPEN表中，每个节点信息还包括指向父节点的返回指针（即父节点地址），其简单结构如表3.1所示。

②CLOSED表:记录将要扩展和已经扩展过的节点。

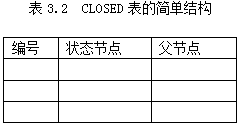
CLOSED表是一种动态数据结构，记录访问过的节点，也叫已扩展节点表，其初始为空表。其简单结构如表3.2所示。

③S0：用表示问题的初始状态。

④G：表示搜索过程所得到的搜索图。

⑤M：表示当前扩展节点新生成的且不为自己先辈的子节点集。

图搜索策略可看作一种在图中寻找路径的方法。初始节点和目标节点分别代表初始数据库和满足终止条件的数据库。求得把一个数据库变换为另一数据库的规则序列问题就等价于求得图中的一条路径问题。研究图搜索的一般策略，能够给出图搜索过程的一般步骤。

3．如何度量问题求解的性能

一般搜索策略可以通过下面四个准则来评价：

①完备性：如果存在一个解答，该策略是否保证能够找到？

②时间复杂性：需要多长时间可以找到解答？

③空间复杂性：执行搜索需要多少存储空间？

④最优性：如果存在不同的几个解答，该策略是否可以发现最高质量的解答？

搜索策略反映了状态空间或问题空间扩展的方法，也决定了状态或问题的访问顺序。在人工智能领域，状态空间图由初始状态和操作符隐含表示的，经常是无限的，它的复杂度根据下面三个值来表达：

①分支因子b：任何节点的后继节点的最大个数。

②最浅的目标节点的深度d。

③状态空间中任何路径的最大长度m。

4．状态空间搜索过程要点

求解一个能够满足目标条件的问题可以表示为搜索一个图以找到一个满足目标状态描述的节点问题。搜索过程的要点如下:

①起始节点:对应于初始状态描述。

②后继节点:把适用于某个节点状态描述的一些算符用来推算该节点而得到的新节点，称为该节点的后继节点。

③指针:从每个后继节点返回指向其父辈节点。

④检查各后继节点看是否为目标节点。

如果搜索是以接近起始节点的程度（由节点之间连结弧线的数目来衡量）依次扩展节点，称为广（宽）度优先搜索。如果搜索时首先扩展最新产生的节点，称为深度优先搜索。

二、图搜索（GRAPHSEARCH）的一般过程

1．图搜索的一般过程

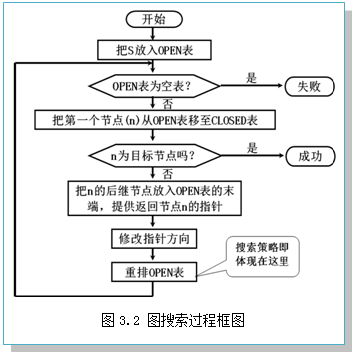图搜索的一般过程如下，其流程图如图3.2所示。

①建立一个只含有起始节点S的搜索图G，把S放到一个叫做OPEN的未扩展节点表中。

②建立一个叫做CLOSED的已扩展节点表，其初始为空表。

③LOOP：若OPEN表是空表，则失败退出。

④选择OPEN表上的第一个节点，把它从OPEN表移出并放进CLOSED表中。称此节点为节点n。

⑤若n为一目标节点，则有解并成功退出，此解是追踪图G中沿着指针从n到S这条路径而得到的（指针将在第7步中设置）。

⑥扩展节点n，同时生成不是n的祖先的那些后继节点的集合M。把M的这些成员作为n的后继节点添入图G中。

⑦对那些未曾在G中出现过的（既未曾在OPEN表上或CLOSED表上出现过的）M成员设置一个通向n的指针。把M的这些成员加进OPEN表。对已经在OPEN或CLOSED表上的每一个M成员，确定是否需要更改通到n的指针方向。对已在CLOSED表上的每个M成员，确定是否需要更改图G中通向它的每个后裔节点的指针方向。

⑧按某一任意方式或按某个探试值，重排OPEN表。

⑨GO LOOP。

1  2