问题:在深度优先搜索中OPEN表的数据结构是( )。
A.栈 B.队列


二、深度优先搜索
下面学习深度优先搜索
1.定义
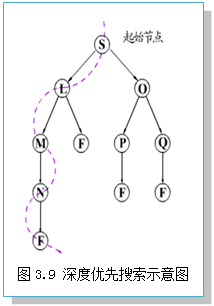 在此搜索中,首先扩展最新产生的(即最深的)节点。深度相等的节点可以任意排列。这种盲目(无信息)搜索叫做深度优先搜索(depth-first search),其示意如图3.9所示。定义节点的深度如下:
在此搜索中,首先扩展最新产生的(即最深的)节点。深度相等的节点可以任意排列。这种盲目(无信息)搜索叫做深度优先搜索(depth-first search),其示意如图3.9所示。定义节点的深度如下:
①起始节点(即根节点)的深度为0。
②任何其它节点的深度等于其父辈节点深度加1。
2.基本思想
从初始节点S0开始,在其子节点中选择一个节点进行扩展并考察它是否为目标节点,若不是目标节点,则在该子节点的子节点中选择一个节点进行考察,一直如此向下搜索。当到达某个子节点,且该子节点即不是目标节点又不能继续扩展时,才选择其兄弟节点进行扩展。节点按后进入OPEN表的顺序排列,即后进入的节点排在表的最前面。
3.特点
新生成的节点优先扩展,直到达到一定的深度限制。若找不到目标或无法在扩展时,回溯到另一节点继续扩展。
①OPEN表:后进先出队列,存放待扩展的节点。
②扩展后的子节点应放入到OPEN表的首部。
4.含有深度界限的深度优先搜索算法
为了避免考虑太长的路径(防止搜索过程沿着无益的路径扩展下去),往往给出一个节点扩展的最大深度设置一个深度界限。任何节点如果达到了深度界限,那么都将把它们作为没有后继节点处理。
含有深度界限的深度优先搜索算法如下:
①把起始节点放到OPEN表中。如果该起始节点为一目标节点,则求得一个解答。
②如果OPEN为一空表,则失败退出。
③把第一个节点(节点n)从OPEN表移到CLOSED的扩展节点表。
④如果节点n的深度等于最大深度,则转向步骤②。
⑤扩展节点n,产生其全部后裔,并把它们放入OPEN表的前头。如果没有后裔,转向步骤②。
⑥如果n的任一个后继节点是个目标节点,则找到一个解答,成功退出;否则转向第②步。
有界深度优先搜索算法的程序框图如图3.10所示。
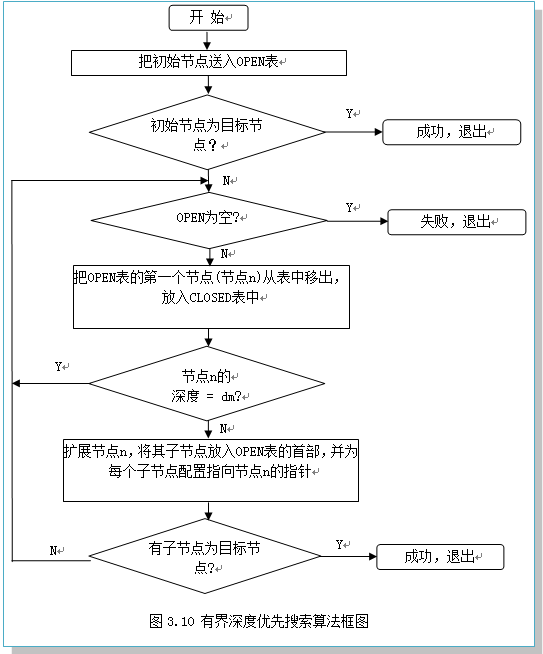


有界深度优先搜索方法能够保证在搜索树中找到一条通向目标节点的最短途径吗?
