您的当前位置是：第四章 计算智能>>学习内容>>知识点四

二、遗传算法的求解步骤

1．遗传算法的特点

①遗传算法是对参数集合的编码而非针对参数本身进行进化；

②遗传算法是从问题解的编码组开始而非从单个解开始搜索；

③遗传算法利用目标函数的适应度这一信息而非利用导数或其它辅助信息来指导搜索；

④遗传算法利用选择、交叉、变异等算子而不是利用确定性规则进行随机操作。

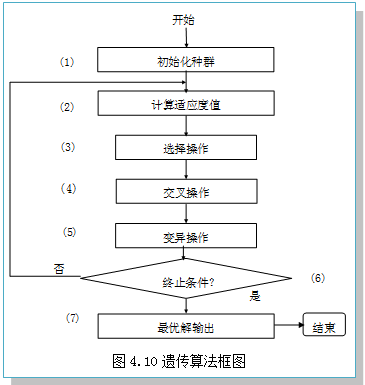2.遗传算法的框图

简单遗传算法框图如图4.10所示，其求解步骤如下：

①初始化种群;

②计算种群上每个个体的适应度值；

③按由个体适应度值所决定的某个规则选择将进入下一代的个体；

④按概率Pc进行交叉操作；

⑤按概率Pm进行变异操作；

⑥若没有满足某种停止条件，则转第②步，否则进入下一步。

⑦输出种群中适应度值最优的染色体作为问题的满意解或最优解。

例4.8 用遗传算法求函数f（x）=x²的最大值，其中x为[0，31]间的整数。

解：这个问题本身比较简单，其最大值很显然是在x=31处。但作为一个例子，它有着较好的示范性和可理解性。

按照遗传算法，其求解过程如下：

①编码

由于x的定义域是区间[0，31]上的整数，由5位二进制数即可全部表示。因此，可采用二进制编码方法，其编码串的长度为5。

例如，用二进制串00000来表示x=0,11111来表示x=31等。其中的0和1为基因值。

②生成初始种群

若假设给定的种群规模N=4，则可用4个随机生成的长度为5的二进制串作为初始种群。再假设随机生成的初始种群（即第0代种群）为：

S₀₁=0 1 1 0 1    S₀₂=1 1 0 0 1

S₀₃=0 1 0 0 0    S₀₄=1 0 0 1 0

③计算适应度

要计算个体的适应度，首先应该定义适应度函数。由于本例是求f（x）的最大值，因此可直接用f（x）来作为适应度函数。即：

f（s）=f（x）

其中的二进制串s对应着变量x的值。根据此函数，初始种群中各个个体的适应值及其所占比例如下表所示。

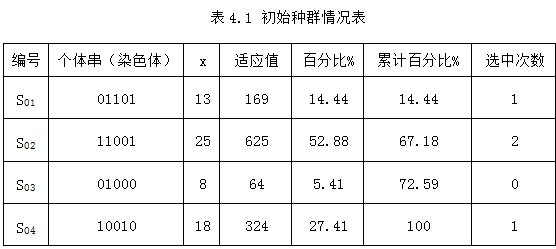
可以看出，在4个个体中S02的适应值最大，是当前最佳个体。

④选择操作

假设采用轮盘赌方式选择个体，且依次生成的4个随机数（相当于轮盘上指针所指的数）为0.85、0.32、0.12和0.46，经选择后得到的新的种群为：

S₀₁=10010

S₀₂=11001

S₀₃=01101

S₀₄=11001

其中，染色体11001在种群中出现了2次，而原染色体01000则因适应值太小而被淘汰。

⑤交叉

假设交叉概率Pc为50%，则种群中只有1/2的染色体参与交叉。若规定种群中的染色体按顺序两两配对交叉，且有S01与S02交叉，S03与S04不交叉，则交叉情况如下表所示。

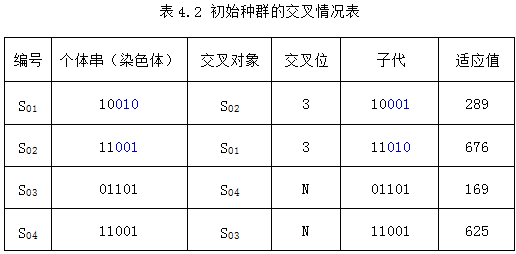
可见，经交叉后得到的新的种群为：

S₀₁=10001

S₀₂=11010

S₀₃=01101

S₀₄=11001

⑥变异

变异概率Pm一般都很小，假设本次循环中没有发生变异，则变异前的种群即为进化后所得到的第1代种群。即：

S₁₁=10001

S₁₂=11010

S₁₃=01101

S₁₄=11001

然后，对第1代种群重复上述④-⑥的操作

对第1代种群，同样重复上述④-⑥的操作。其选择情况下表所示。

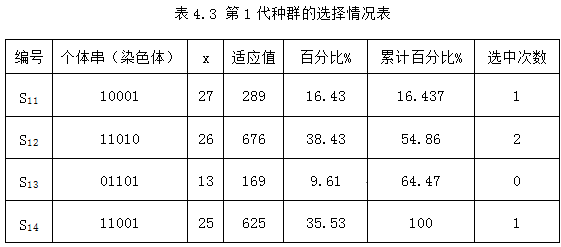
其中若假设按轮盘赌选择时依次生成的4个随机数为0.14、0.51、0.24和0.82，经选择后得到的新的种群为：

S₁₁=10001

S₁₂=11010

S₁₃=11010

S₁₄=11001

可以看出，染色体11010被选择了2次，而原染色体01101则因适应值太小而被淘汰。

对第1代种群，其交叉情况如下表所示。

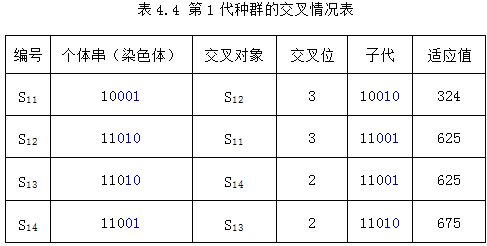
可见，经交叉后得到的新的种群为：

S₁₁=10010

S₁₂=11001

S₁₃=11001

S₁₄=11010

可以看出，第3位基因均为0，已经不可能通过交配达到最优解。这种过早陷入局部最优解的现象称为早熟。为解决这一问题，需要采用变异操作。

对第1代种群，其变异情况如下表所示。

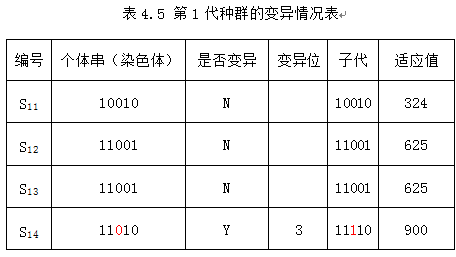
它是通过对S14的第3位的变异来实现的。变异后所得到的第2代种群为：

S₂₁=10010

S₂₂=11001

S₂₃=11001

S₂₄=11110

接着，再对第2代种群同样重复上述④-⑥的操作：

对第2代种群，同样重复上述④-⑥的操作。其选择情况如下表所示。

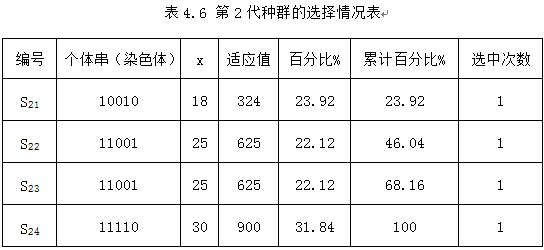
其中若假设按轮盘赌选择时依次生成的4个随机数为0.42、0.15、0.59和0.91，经选择后得到的新的种群为：

S₂₁=11001

S₂₂=10010

S₂₃=11001

S₂₄=11110

对第2代种群，其交叉情况下表所示。

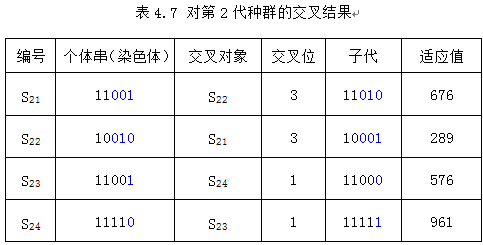
这时，函数的最大值已经出现，其对应的染色体为11111，经解码后可知问题的最优解是在点x=31处。

求解过程结束。

1  2