您的当前位置是：实践交流>>实践主题二

【实践内容】

利用博弈树搜索中的α-β剪枝技术求解一字棋游戏的每个最佳走步

【实践任务】

一字棋游戏：设有一个三行三列的棋盘，两个棋手轮流走步，每个棋手走时往空格上摆一个自己的棋子，谁先使自己的棋子成三子一线为赢。利用博弈树搜索中的α-β剪枝求解一字棋游戏的每个最佳走步，以某个棋局为例，给出求解过程的描述。

【实践要求】

小组成员合作交流，提交问题的求解方案。同时关注成果交流版块，积极参与其他小组成果的讨论。

【成果交流】

学生成果案例
设程序方MAX的棋子用（×）表示，对手MIN的棋子用（○）表示，MAX先走。静态估计函数f（P）规定如下：
1．若P是MAX的必胜局，则f（P）=+∞；
2．若P是MIN的必胜局，则f（P）=-∞；
3．若P对MAX、MIN都是胜负未定局，则
      f（P）=e（+P）－e（-P）
其中，e（+P）表示棋局P上有可能使×成三子一线的数目；e（-P）表示棋局P上有可能使○成三子一线的数目。
以第一步走棋为例，图1是利用α-β剪枝方法求解MAX第一步棋最佳走法的剪枝过程。图中数字表达式是节点静态估计值的计算过程。

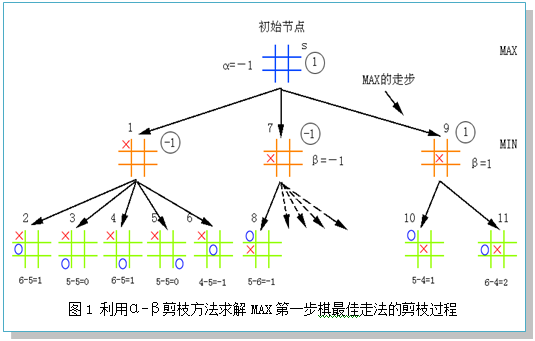
【教师点评】

在博弈树的极大极小搜索方法中，由于要先生成指定深度以内的所有节点，其节点数将随着搜索深度的增加成指数增长。这极大地限制了极大极小搜索方法的使用。能否在搜索深度不变的情况下，利用已有的搜索信息减少生成的节点数呢？
α-β剪枝技术采用有界深度优先策略，当生成规定深度的节点时，计算叶节点的静态估值，并倒推非端节点的估值。根据倒推结果，在非端节点的向下分枝中，剪掉那些目前未知，但无论如何都不会改变非端节点倒推值的未扩展分枝。因此，有效地提高了搜索效率。