

【实践内容】
利用遗传算法求解旅行商问题
【实践任务】
旅行商问题(TSP)可以具体描述为:已知n个城市之间的相互距离,现有一个推销员从某一个城市出发,必须遍访这n个城市,并且每个城市只能访问一次,最后又必须返回到出发城市,如何安排他对这些城市的访问次序,可使其旅行路线的总长度最短。给出问题的求解方案描述。
【实践要求】
小组成员合作交流,提交问题的求解方案。同时关注成果交流版块,积极参与其他小组成果的讨论。
【成果交流】
学生成果案例
1.编码
采用符号编码,编码形式如下:
w1w2…wn
由于是回路,记wn+1=w1。它其实是1,…,n的一个循环排列。要注意w1,w2,…,wn是互不相同的。
2.适应度函数
适应度函数采用如下方法定义:
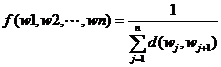
3.选择方案
采用“轮盘赌”选择方案。
4.交叉操作
采用部分匹配交叉操作(Partially Matched Crossover,PMX),随机选取两个交叉点,以便确定一个匹配段,根据两个父母个体中两个交叉点之间的中间段给出的映射关系生成两个子个体。
例如,对下面两个父母个体的表示,随机地选择两个交叉点“|”。
P1:(1 2 3 | 4 5 6 7 | 8 9)
P2:(4 5 2 | 1 8 7 6 | 9 3)
首先,两个交叉点之间的中阶段交换,得到:
O1:(x x x | 1 8 7 6 | x x)
O2:(x x x | 4 5 6 7 | x x)
其中,“x”表示暂未定义码,得到中阶段的映射关系,有
1<->4,8<->5,7<->6,6<->7
然后,对子个体1和子个体2中“x”部分,分别保留从其父母个体中继承未选定的城市码2,3,9得到:
O1:(x 2 3 | 1 8 7 6 | x 9)
O2:(x x 2 | 4 5 6 7 | 9 3)
然后,根据中间段的映射关系,对于上面子个体1的第一个“x”,使用最初父码“1”,由1<->4交换得到第一个“x”为4,类似地进行操作,最终得到的子个体为:
O1:(4 2 3 | 1 8 7 6 | 5 9)
O2:(1 8 2 | 4 5 6 7 | 9 3)
如果映射关系中存在传递关系,即备选交换有多个码,则选择此前未确定的一个码作为交换。如:
P1:(1 2 3 | 4 5 6 8 | 7 9)
P2:(4 5 2 | 1 8 7 6 | 9 3)
中间段的映射为:
4<->1,5<->8,6<->7,8<->6
交叉后:
O1:(4 2 3 | 1 8 7 6 | 5 9)
O2:(1 7 2 | 4 5 6 8 | 9 3)
5.变异操作
随机产生一个1到n之间的数k,决定对回路中的第k个城市的代码wk作变异操作,又产生一个1到n之间的数w替代wk,并将wk加到尾部,得到:
w1w2…wk-1wwk+1…wnwk
这个串中有n+1个数码,数w在此串中重复了,必须删除与数w相重复的数以得到合法的个体。
【教师点评】
遗传算法(Genetic Algorithm,简称GA)的基本思想是基于Darwin进化论的Mendel的遗传学说,它将问题的解集看作一个种群,通过不断的选择、交叉、变异等遗传操作,使解的质量越来越好。遗传算法最早由美国J.H.Holland教授提出,其主要特点是简单、通用、鲁棒性强,尤其适用于传统搜索算法难以解决的复杂和非线性问题。隐含的并行性和全局搜索性是遗传算法的两大显著特征。
一般遗传算法的主要步骤如下:
1.随机产生一个由确定长度的特征字符串组成的初始群体。
2.对该字符串群体迭代的执行下面的步①和②,直到满足停止标准:
① 计算群体中每个个体字符串的适应值;
② 应用复制、交叉和变异等遗传算子产生下一代群体。
3.把在后代中出现的最好的个体字符串指定为遗传算法的执行结果,这个结果可以表示问题的一个解。
在应用遗传算法求解具体问题时,需要设计具体问题的编码方案、适应度函数、选择方案、交叉操作和变异操作等。