推断统计是通过借助样本提供的信息，推论总体情况的方法。推断统计主要包括总体参数的估计和假设检验这两部分内容。

一、假设检验的基本步骤

1．提出假设。

如“假设两个总体平均数没有差别”，其数学符号为：“H0：μ1=μ2”，这种对总体所作的“无差别”的假设，称为“零假设”或称虚无假设，用符号“H0”表示。（μ1，μ2表示两个总体的平均数）。与此同时，实际上存在第二种假设，“两个总体平均数有差别”，其符号为：“H1：μ1≠μ2”，称为备择假设。显然，虚无假设与备择假设是两个对立的假设，肯定此，必否定彼。

2．计算出检验统计量的具体值。

代入相应的公式，计算出检验统计量的具体值（如后面将介绍的Z值、T值、X2值）。

3．做出统计推断。

根据“小概率事件实际上不可能性”原理，研究H0成立的概率。如果H0的概率P＞0.05，表示零假设不是一个小概率事件，否定备择假设H1，则H0成立，即“μ1=μ2”。如果H0的概率p＜0.05，表明零假设是一个小概率事件，H0不成立，就肯定备择假设H1的成立，从而确定“μ1≠μ2”。

二、常用的检验方法

检验方法分为参数检验方法和非参数检验方法。在学前教育研究领域，最为常用的检验方法是参数检验中的z检验、t检验和非参数检验中的X2检验。

1．Z检验当两个独立无关的大样本(即样本容量大于30)时使用。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。公式为：

（11.13）

[例6]  从某市的六岁儿童中随机抽测100个男孩和80个女孩的身高，所得结果如下表，根据这次抽样测量的结果，该市男女儿童身高是否存在显著差异？

表11—7             男女儿童身高测量结果

解：抽取的两个样本均大于30，属两个独立大样本平均数差异的显著性检验，用Z检验。

检验步骤：

（1）提出假设，H0：μ1=μ2，H1：μ1≠μ2

（2）计算统计量，代人Z值公式

（3）计算出的Z值与下表进行对照，做出判断：

由于1.96＜2.39＜2.58，故0.01＜P＜0.05，根据Z检验的规则作出判断：在0.05的显著性水平上拒绝零假设，接受备择假设，即该市男女六岁儿童的身高有显著差异。

2．t检验

（1）独立样本t检验

当两个样本是相互独立的，且是小样本时（即样本容量小于30）使用。公式为：

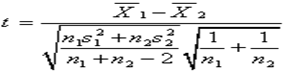
（11.14）

特别指出的是，这个公式的使用条件是：总体正态分布，样本随机抽取，相互独立；总体方差未知，但差异不显著。

[例7] 用甲、乙两种不同风格的教学设计方案分别在两个小组进行教学实验，甲组12人，乙组14人，实验结束两个小组的测验成绩如表11—8所示。

两种教材的实验效果是否有显著差异？（假设测验成绩总体服从正态分布）

表11-8两小组测验成绩

解：①建立假设，H0：μ1=μ2，H1：μ1≠μ2

②计算统计量t

首先依据上述资料求得：S1=3.68 ；S2=5.49 ，已知n1=12，n2=14，将上述各值代入公式得

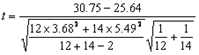＝2.63

（2）相关样本t检验

当两个样本的平均数并非独立的，而是存在成对的，或是存在相互关联的关系时使用。公式为：

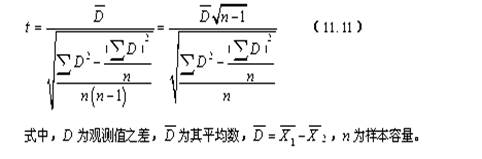
（11.15）

[例8]  某班利用多媒体教学前后学生的学习兴趣测量得分如下表，问前后两次测量结果间是否存在显著差异？

表11-9学习兴趣测量得分比较

利用后 利用前	30 17	30 25	34 37	37 27	38 24	35 18	39 32	20 22	30 28	34 27
	13 169	5 25	-3 9	10 100	14 196	17 289	7 49	-2 4	2 4	7 49

解：建立假设，H0：μ1=μ2，H1：μ1≠μ2

[例9]  某学校为了了解家长对某项教改实验的态度，对60位家长进行了一次调查，调查结果如表11—10，问三种态度的人数是否有显著差异?

表11-10 家长对某项教改实验的态度

态度	赞   成	无所谓	反   对
实测人数	30	16	14

解：

缩节《X2值表》

Df	0.05	0.01
1	3.841	6.635
2	5.991	9.210
3	7.815	11.345
4	9.488	12.277
5	11.070	15.068

由于5.991＜7.6＜9.210,即0.01＜P＜0.05，因此，在0.05显著性水平上，拒绝零假设,认为家长对这项教改实验的态度有显著差异。

通过对教育研究资料推断统计的学习，你是否真正了解与掌握了其中的内容呢？接下来让我们一起进入边学边练。

• 1．（ ）是通过借助样本提供的信息，推论总体情况的方法。（单选）
  A.推断统计
  B.描述统计
  C.分析统计
  D.概括统计
  
  教师解析：答案A。推论就是推断、预测。
• 2． 假设检验从总体上可分为（ ）。（多选）
  A.参数检验
  B.非参数检验
  C.X2检验
  D.Y2检验
  
  教师解析：答案为A、B。假设检验从总体上可分为参数检验和非参数检验，相应的检验方法则分为参数检验方法和非参数检验方法。
• 3. 下列属于参数检验的有（ ）。（多选）
  A.Z检验
  B.T检验
  C.X2检验
  D.Y2检验
  
  教师解析：正确答案为A、B。在教育研究领域，最为常用的检验方法是参数检验中的Z检验、T检验和非参数检验中的X2检验。