描述统计是通过对由实验或观察、调查所得到的数据进行整理并计算其特征数，以描述数据的分布特征，把握数据全貌的方法。一般地说，数据的整理是借助对数据的排序、分组、制作图表等方法进行的，而数据特征数的计算，是通过求数据的平均数、标准差、相关系数等以求了解数据的集中趋势、离散程度以及相关情况等。在教育研究中，有很多情况需要运用描述统计的方法，以便使研究科学合理地进行，得到正确的结论。

一、集中量数

集中量数是用来描述数据分布集中趋势的统计量。它能反映一组数据的分布中，大量数据向某一点集中的情况。常用的集中量数有算术平均数、中位数和众数，其中，在教育研究中，运用较多的是算术平均数。

（一）算术平均数

1．算术平均数的含义

算术平均数是所有观察数据的总和除以数据个数所得的商，简称为平均数或均数、均值。它反映某一现象的数量标志在一定条件下的一般水平，通常用符号 表示，读作x杠，有时也用M表示。它的计算公式为：

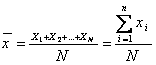
（11.1）

式中，N表示数据的个数；

X1,x2,……表示变量X的各次观测结果；

是希腊字母，表示连加求和。

2．算术平均数的计算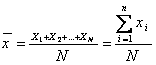

（1）原始数据求平均数

当一组数据是原始数据时，就把它们直接代入公式11．1来求平均数。

[例1]已知5名学生的身高（单位：cm）分别为：98，99，105，102，101，求他们的平均身高是多少？

解：将5名学生的身高代入公式（11.1）得：

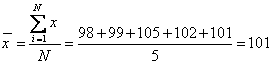（cm）

（2）分组资料求平均数

如果一组原始数据编成了次数分布表，已经看不到原始数据，在这种情况下，一般采用的方法是：各组组中值乘以各组次数，求其和，再除以总次数，所的结果即为这组数据算术平均数的近似值。其计算公式为：

（11.2）

式中，x为各组组中值；f为各组次数；N为总次数。

[例2]请利用表11—2的资料计算算术平均值。

表11—2 某小班40名儿童身高的平均数计算表（CM）

需要指出的是，用原始数据与根据次数分布表计算的平均数，二者在数值上有少许差异，这是由于用次数分布表计算平均数时，先假设落入各区间内的数据均匀分布在组中值上下，而实际情况不一定是这样的，从而造成了一定的计算误差。从计算的实际结果来看，二者相差不是很大，并不会影响以后的统计分析。

（3）加权算术平均数

在进行资料分析时，也会遇到这样的情况：一组同质数据中某些数多次重复出现，或参与计算平均数的每一个数据，在总体中的地位并不一样，即各个数据在其总体中所占的权重不同。这时，必须使用加权算术平均数。

所谓加权算术平均数，是指一组同质数据中每一数值与其对应权数乘积的总和，再除以权数总和所得之商。其公式为：

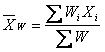
（11.3）

式中，Wi为相应的权重(=1、2、3…)。

[例3]某幼儿园有4个小班，一班45人，二班40人，三班有42人，四班38人。各班幼儿平均身高分别为78.5、79、80.75、82.5。问如何估计该幼儿园小班全体幼儿的平均身高？

解：因为已知各班人数以及各班的平均身高，估计全年级的总体水平要用加权算术平均数。

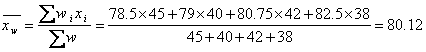
3．平均数的优点和缺点

算术平均数是最重要、最完善的集中量数，它具有以下优点：

（1）反应灵敏。观测数据中任何一个数值或大或小的变化，甚至细微的变化，在计算平均数时，都能反映出来。

（2）计算严密。计算平均数有确定的公式，不管何人在何种场合，只要是同一组观测数据，计算的平均数都相同。

（3）计算简单。计算过程只是应用简单的四则运算。

（4）简明易解。平均数概念简单明了，较少数学抽象，容易理解。

（5）适合于进一步用代数方法演算。在求解其他统计特征量时，如方差、标准差等的计算时，都要应用平均数。

（6）较少受抽样变动的影响。观测样本的大小或个体的变化，对计算平均数影响很小。在来自同一总体逐个样本的集中量数中，平均数的波动通常小于其他量数的波动，因此，它总是最可靠、最正确的量数。

但是，算术平均数也有一些缺点，在一定程度上限制了它的应用。比如，计算中，常常会因少数极端值的影响而大大改变其数值，削弱其代表性。有时，在计算平均数时除去极端值，对数据集中趋势的估计效果会更好，特别是数据不属于正态分布时，这种方法更为妥当。在实际生活中，大家常常会看到，在各种比赛中，计算某一选手的平均成绩时，往往是去掉一个最高分和一个最低分，然后再算平均值，这样的做法更科学。

（二）中位数

1．中位数的含义

中位数是按顺序排列在一起的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比它大，有一半的数据比它小。这个数可能是数据中的某一个，也可能根本不是原有的数。中位数，简称中数。

中位数是根据全部观察数值数目确定的，简单明了，便于计算。一般用于下列情况：①由于中位数的计算不需要每个数据都参加，较少受极大值和极小值的影响。因此，当一组观测结果中出现两个极端数目时，往往采用中位数代表集中趋势；②当次数分布的两端数据或个别数据不清楚时，只能取数据的中位数作为集中趋势的代表值；③当需要快速估计一组数据的代表值时，也常用中位数。

但是，中位数不能用代数法计算，用中位数乘以总次数并不能得出原数值的总和。中位数不像平均数那样容易被人理解，其用处也不如平均数那么广泛。

2．中位数的计算方法

中位数的计算方法是，先把所有数据按照大小顺序排列并编号，然后分三种情况处理：

①当数据的个数n为奇数时，中位数就是正中位置的那个数，即位于第号的数。

②当数据的个数n为偶数时，中位数就是中间两个数值的平均数，即位于第和号的两数的平均数。例如，表11—3中有8个数据，因为，，故中位数为第4号和第5号数据的平均数，即。

表11—3

数据	20	41	53	56	74	79	86	92
编号	1	2	3	4	5	6	7	8

可见，当数据个数为奇数时，中位数是原始数据中的一个数值，而当数据个数为偶数时，求得的中位数并不存在于原来的数据中。

③当有重复数据，或者由于数据过多，需要归类计算中数时，需要借助相应的公式进行。

（三）众数

众数是指一组数据中，出现频数最多的那个数的数值。用表示众数。

众数在工作中运用得比较少，主要在以下情况中使用：①需要快速而粗略地寻找一组数据的代表值时；②需要利用算术平均数、中位数、众数三者的关系来粗略地估计频数分布的形态时；③数据分布中有两极端的数值时。

2．众数的计算方法

众数可以通过观察来找到。在一组原始数据中，出现的频数最多的那个数值就是众数。例如，在5，4，5，2，6，5这组数据中，5出现的频数最多，这组数据的众数就是5。

在频数分布表中，频数最多一组的组中值就是众数。如表11—2资料中，98就是众数。

二、差异量数

差异量数是表示一组数据的差异情况或离散程度的量数。

有时，两组数据分布，其集中趋势相同而离散趋势不同，或者离散趋势相同而集中趋势不同，在这种情况下，就不能说这两种分布是完全相同的。只有对集中量数与差异量数都作出考察，才能比较清晰地了解数据分布的全貌。差异量数可以反映集中量数所具有的代表性。差异量数越大，集中量数代表性越小；差异量数越小，集中量数代表性越大；差异量数为0，集中量数即该数值本身。可见，考察差异量数，有助于我们理解集中量数。

差异量数一般包括全距、四分差、平均差、标准差、差异系数等。在数据统计分析中常用的是标准差和差异系数。

（一）标准差

标准差是指一组数据中每个数值与该组数据平均数离差的平方和之平均数的平方根。其计算公式为：

（11．4）

为了计算简便，可用下列公式：

（11.5）

式中，表示要把每一个数首先平方，然后相加，表示先把全部数据相加，然后再平方。

标准差是最重要、最完善的差异量数，常与平均数一起使用，以描述数据分布的整体情况。

标准差是带有与原观测值相同单位的量数，适合于对所观测的样本水平比较接近，且使用同一测验对同一特质进行测量的不同样本之间离散程度的比较，所以标准差被称为绝对差异量数。它对单位不同，或单位虽相同但平均数相差较大的样本之间的差异程度却无法比较。这时要选用相对差异量数，最常用的就是差异系数。

（二）差异系数

差异系数又称相对差异量数，或相对标准差，是同一组数据标准差与平均数的比率。其计算公式为：

（11.6）

差异系数是用来比较同一团体或个人在不同测量单位的测验中的分数，或者比较不同团体进行同一种观测获得的数据。例如，比较三岁组儿童与六岁组儿童语言表达能力的差异程度的大小；比较一组三岁儿童在身高和体重方面的差异程度的大小。差异系数大表示该组数据离散程度大，差异系数小表示该组数据离散程度小。

[例4]在同一语言表达测验中，一组儿童的平均分数为60分，标准差为4.02分，二组儿童的平均分数是80分，标准差为6.04分，问这两个年龄组的测验分数中，哪一个分散程度大？

解：

7.55%＞6.7%，所以，二组儿童测验分数的离散程度大。

一般地，差异系数值常在5%~35%之间，如果大于35%，可怀疑所求得的平均数是否失去意义，如果小于5%，可怀疑平均数与标准差的计算是否有误。

三、相关关系

平均数和标准差都是描述一组变量特征的量数，而事物之间总是相互联系的，孤立的事物是不存在的。这种相互联系的关系大体上有三种：因果关系（如，学习努力，成绩就好）、共变关系（有联系的两事物都与第三现象有关）、相关关系，即两类现象在发展变化的方向与大小方面存在一定关系，但不能确定哪个是因，哪个是果，如身高与体重、学习成绩与思想品德等的相互关系。这就需要了解描述变量间关系特征的量数，即相关系数。

相关就是指两组或两组以上资料或配对变量之间的相互关系。

1．相关类型

（1）正相关与负相关

按照两个变量相互伴随变化的方向，可分为正相关和负相关。

正相关就是两个变量的变化方向一致的相关，即一个变量值变大时，另一个变量值也随之变大；一个变量值变小时，另一个变量值也随之变小。例如，身高与体重的关系，学习能力与学习成绩的关系。负相关就是两个变量的变化方向相反的相关，即一个变量值变大时，另一个则变小；一个变量值变小时，另一个则变大。例如，身体状况与生病率的关系。

（2）完全相关、不完全相关和零相关

按照变量间相关程度分，可分为完全相关、不完全相关和零相关。

完全相关是指相关联的两个变量，如果一个变量变动时，另一个变量对应值随着成比例地变化。存在完全相关的两个变量，其成对观测值的坐标点在一条直线上。在教育与心理研究中，完全正相关或完全负相关关系是很少有的，几乎都是不完全相关关系。存在不完全相关关系的两个变量，其坐标点不在一条直线上。零相关是指两个变量间没有关系，即一个变量的值无论怎样变化，另一个变量的对应值都不改变或无规律地改变。

相关程度的大小用相关系数表示，的取值范围为。r＞0为正相关，r＜0为负相关，r=0为零相关。图11—5就是正相关、负相关和零相关的示意图。

图11-5相关的三种情况

2．相关系数的求法

描述两个变量之间的相关程度时，最常用的相关系数是积差相关系数。积差相关系数的计算公式是：

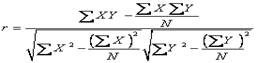
（11.7）

或者

（11.8）

式中

[例5]为了研究儿童性格发展与家庭教育之间的关系，随机对12名儿童的性格特点及其家长的教育情况进行了调查，得到每名儿童的性格总分（X）和每个家庭的教育总分（Y），如表11—5所示，求儿童性格总分与家庭教育总分之间的积差相关系数。

表11—412名儿童的性格总分与家庭教育总分

表11—5儿童性格和家庭教育分数相关计算表

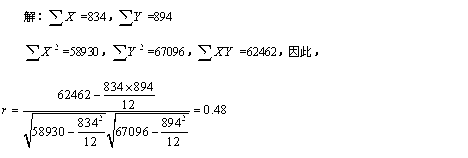
3．解释和应用相关系数应注意的问题

（1）存在相关，仅意味着变量间有关联，并不一定是因果关系。即使存在因果关系，也不能从其相关中判断哪个是原因哪个是结果，要了解何为原因和为结果，还必须进一步研究。

（2）相关关系不是百分率，也不等距，因此，不能对相关系数直接进行加、减、乘、除运算。

（3）相关系数r受变量取值区间大小及观测值个数的影响较大，变量的取值区间越大，观测值的个数越多， r受抽样误差的影响越小，结果越可靠。因此，在研究事物间关系时，应适当加大变量的取值区间，并获得足够的观测值，一般要求样本容量在30以上或更多些。在比较两相关系数大小时，也必须考虑到观测值数目上的差异。

（4）相关系数的正负号表示相关方向，其绝对值表示相关程度的高低。通过实际观测值计算的相关系数，须经过显著性检验确定其是否有意义。在相关系数有意义的前提下，一般根据表11—6对其进行解释。

表11-6|r |的取值与相关程度

注释：

1. 组中值：是上下限之间的中点数值，以代表各组标志值的一般水平。组中值并不是各组标志值的平均数，各组标志数的平均数在统计分组后很难计算出来，就常以组中值近似代替。组中值仅存在于组距式分组数列中，单项式分组中不存在组中值。

2. 集中量数：描述所搜集到的资料里各分数之集中情形的最佳代表值，也是描述一个团体中心位置的一个数值。集中量数有多种，包括算术平均数、中数、众数、加权平均数、几何平均数、调和平均数等。

教育学：一组数据中大量数据集中在某一点或其上下的情况说明了该组数据的集中趋势，描述集中趋势的统计指标叫做集中量数。

3. 集中趋势：在统计学中是指一组数据向某一中心值靠拢的程度，它反映了一组数据中心点的位置所在。

集中趋势测度就是寻找数据水平的代表值或中心值，低层数据的集中趋势测度值适用于高层次的测量数据，能够揭示总体中众多个观察值所围绕与集中的中心，反之，高层次数据的集中趋势测度值并不适用于低层次的测量数据。

4. 离散趋势：计量资料的频数分布有集中趋势和离散趋势两个主要特征。仅仅用集中趋势来描述数据的分布特征是不够的，只有把两者结合起来，才能全面地认识事物。我们经常会碰到平均数相同的两组数据其离散程度可以是不同的。一组数据的分布可能比较集中，差异较小，则平均数的代表性较好。另一组数据可能比较分散，差异较大，则平均数的代表性就较差。描述一组计量资料离散趋势的常用指标有极差、四分位数间距、方差、标准差、标准误差和变异系数等，其中方差和标准差最常用。

5. 标准差：（Standard Deviation） ，中文环境中又常称均方差，但不同于均方误差（mean squared error，均方误差是各数据偏离平均数的距离平方的平均数，也即误差平方和的平均数，计算公式形式上接近方差，它的开方叫均方根误差，均方根误差才和标准差形式上接近），标准差是离均差平方和平均后的方根，用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的，标准差未必相同。

6. 差异系数: 差异系数，也称变差系数、离散系数、变异系数，用V表示。它是一组数据的标准差与其均值之比，是测算数据离散程度的相对指标。

差异系数通常用用标准差计算，因此，差异系数也被称为标准差系数。其计算公式为：

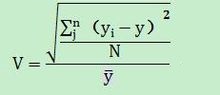
离散系数大，代表其数据的离散程度大，其平均数的代表性就差，反之亦然。

7. 相关系数：相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。

简单相关系数：又叫相关系数或线性相关系数，一般用字母P 表示，用来度量两个变量间的线性关系。

复相关系数：又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如，某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。

典型相关系数：是先对原来各组变量进行主成分分析，得到新的线性关系的综合指标，再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。