一、教育统计的含义与性质

统计是对所考察的事物或现象从量的角度在其全部范围内作总体的把握。统计学是从数量方面研究随机现象总体特征的理论和方法的科学，即是研究如何归类、分析反映事物总体信息的数字资料，并以此为依据，对总体特征进行推断统计的原理与方法的方法论科学。

统计学分为数理统计学和应用统计学两大类。数理统计以概率论为基础，对反映事物特征的数量关系进行抽象，概括出数据分析的模型、原理和方法。应用统计学与具体研究对象密切结合，侧重于数理统计的原理与方法在各个领域的应用。教育统计学是把数理统计的理论与方法应用到教育领域，研究教育现象的一门应用学科，着重介绍数理统计原理和方法在教育实践中应用的适用条件和方法步骤以及统计计算结果的分析与解释，是我们正确认识和研究教育现象数量特征的重要工具。教育统计学的研究对象是在质与量的辨证统一中着重从数量角度去研究教育现象发展变化，探索教育规律。

二、教育统计的内容结构

科学地处理和分析学生成绩的特征，必须从两个方面：一是学生成绩的一般特征和差异情况；另一方面就是学生成绩对教师教学水平的代表程度。这就涉及到描述统计和推断统计两部分内容。

（一）描述统计

描述统计主要是研究如何将调查、实验、观察、日常管理等得到数据资料科学地加以整理、概括和表述，把研究问题或现象的数量特征、分布状态用统计图表或数量指标表示出来，以揭示事物发展变化的一般状况、相互关系等。描述统计包括如何用统计图表描述一组数据的分布情况；如何计算一组数据的特征值；如何分析一事物两种属性间或两种事物之间的相互关系。描述统计是推断统计的基础，它可以用于表示局部的数量特征，也用来表示整体的数量特征。描述统计在日常的教育教学工作和教学管理中经常使用，如分析学科平均成绩、成绩分化情况、优秀率、及格率、教师教学态度与学生学业成就的关系、学校经费使用情况等。

（二）推断统计

推断统计是研究如何利用样本资料，运用统计理论与方法，分析、论证在一定可靠度下总体的数量特征、关系、分布等。统计研究的目的是要获得对样本所在总体的认识，因此推断统计要以描述统计为基础，在描述统计获得的有限信息资料的基础上去进一步推论其所在总体的数量特征，并能说明这种推论结果的可靠性。例如，某研究抽样调查某市城市小学生的近视率为20%，农村小学生的近视率为10%，这两个百分数就作为该研究所获得的城市和农村小学生近视率的估计值，如何估计，需要借助推断统计中参数估计的原理和方法来进行。如果进一步探讨城市小学生的近视率与农村小学生的近视率是否有差异，就要用推断统计中的检验方法。

教育管理和教育科学研究中由巳知去说明未知，由有限去推断无限的问题非常多，没有推断统计提供具体的推断方法，许多问题难以得出科学的结论。本课程主要介绍参数估计和假设检验的具体方法。

三、教育统计中常用的术语

（一）随机现象

教育统计所研究的教育现象是随机现象。在教育观察、实验或调查中所获得的数据资料，在测量、调查之前，不能准确地预料会获得什么样的数值。在同样条件下，反复多次进行同一试验，或多次观测同一现象，所得结果并不完全一样，在每次试验或观测之前不能确切预料将出现什么结果，这样的现象称之为随机现象。随机现象有三个特点：第一、其结果至少有两个；第二、至于那种结果出现，人们事先并不知道；第三，在相同条件下反复观察或试验，呈现出一定的规律性。例如，如随机抽取30名四年级学生进行阅读能力测试，结果可能是“没有不及格”，可能是“有一个不及格”，也可能是“有两个不及格”等。

（二）总体和样本

总体又称全域，指具有某种特征的一类事物的全体。构成总体的每个基本单位称为个体。把按一定方法从总体中抽取的与总体性质相同的有代表性的一部分个体所构成的新的集合称为样本。如果所研究的总体的对象数目是有限的，则称为有限总体，用N来表示个体数目：若总体中包含的个体的数目是无限的，则称为无限总体。样本是从总体中抽取出来的，作为总体代表的一部分单位组成的集合体。样本中所含个体的数目称为样本容量。样本可以是实验中所选取的一组被试的实验结果，或一个被试的多次结果等。一个总体可以组成多个样本，而抽取样本要排除主观因素。例如某研究者要调查当前长春市幼儿教师的学历及职业认同度，在这里，长春市所有的幼儿老师就是总体，是一个有限总体。按照幼儿园的类型从长春市所有幼儿教师中随机抽取500名，这就是一个样本。

用来说明总体的样本，一定要对总体有代表性。而要获得对总体有充分代表性的样本，就必须注意两点，一是样本容量要足够大，二是样本要随机抽取。样本容量越大，样本对总体的代表性越强，依其进行推断的可靠性越高；样本小时，个别数值的变化会对整个统计结果发生重大影响。但并不是样本越大越好，太大会给搜集资料和计算带来麻烦。因此，样本容量的大小一般依研究问题的精确度要求和可提供的统计方法及实际可能而定。统计上，一般称样本容量大于或等于30时为大样本，小于30时为小样本。由于样本的大小不同，采取的统计方法也不同。在教育管理与研究中，样本容量一般要大于50。

（三）参数与统计量

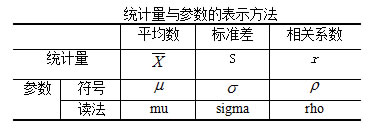
统计学上把代表总体特征的量数称之为参数，如总体平均数、总体方差和总体相关系数等，一般用希腊字母表示。参数是反映总体一般特征的量数，可以由总体观测值直接求得。但教育中总体往往太大，无法通过每个观测值求得参数，因此，参数通常以相应的样本统计量对参数进行估计与推断。代表样本特征的量数称之为样本统计量，一般用英文字母来表示。样本统计量是由样本观测值计算得到的，样本不同，样本统计量也会不同，因此，统计量本身也是一个随机变量。如了解2012届全国高三学生的外语水平，则全国高三学生外语统考成绩的平均数、标准差、及格率等都是高三学生外语成绩这个总体的参数。但是，总体太大，无法通过每个观测值求得参数，必须通过样本统计量去估计总体特征。各个省按照地区经济发展水平、学校类型等指标从本省高三中抽取一个样本，这些样本的学生外语成绩的平均数、标准差、及格率等都是统计量，由这些样本可以合成一个更大的样本，计算统计量，作为全国高三学生外语成绩的估计值。样本来自总体，在一定程度上反映着总体特性，但它只是总体的一部分，因此样本统计量和总体参数间总会有一定差异，样本容量越大，样本统计量和总体参数间的差异越小。

统计量与参数的表示方法

（四）自由度

自由度是指统计运算与推断中变量值独立自由变化的数目，一般用符号表示。对于任一随机变量的取值变化，在总体上，我们称它是无任何限制的，每个随机变量的取值都是自由变化的，其自由度也是无限的。但在有限样本中，统计量的计算往往受到一定的限制，会失掉一定的自由度。自由度失去的多少取决于计算统计量时实际受约束条件的多少，在后面将学习到的统计推断中，其自由度根据不同情况取不同的值。