统计表就是把统计资料汇总的结果整理成表格，它是统计资料最主要的表现形式，可使大量的统计数据系统化、直观化，同时便于比较分析和进一步计算统计量。统计表也是自下而上定期地向上级行政部门传送统计资料的重要载体。

一、统计表的结构与种类

（一）统计表的结构

统计表一般由表序、标题、标目（又称项目，有横标目和纵标目之分）、线条、数字、表注构成，如表2-2所示。

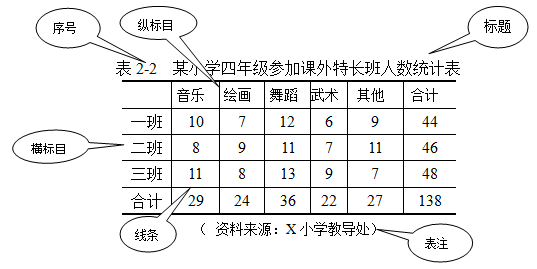
标题是指统计表的名称，写在表上端中间位置，一般是陈述句目是指统计表的横行标题和纵列标题；容。表中表示项目的统计数据是统计表的主体。表的序号、说明、数据来源等可视具体情况适当取舍。

（二） 统计表的种类

按分类标志的标准和数目，统计表可分为简单表、分组表和复合表。

1．简单表。即统计资料的标目未经任何分组，只按一个标志简单列出调查单位（名称、地点）、时序（年份、月份）或统计指标名称的统计表。学校常规性数据资料一般用简单表整理和存档。

表2-3 某农村小学各年级在校生人数统计表

2．分组表。即将统计资料的标目按一个标志（品质或数量）进行分组列成的统计表，一般反应一种教育现象的发展变化情况或问题。

表2-4 初二三班53名学生期末考试成绩统计表

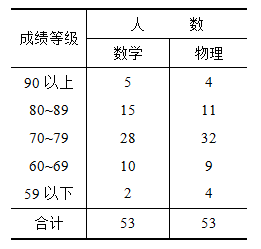
3．复合表。按两个或两个以上标志分组列成的统计表，主要用于比较事物之间的关系、差别及规律，如下面这个统计表可以反应课外特长班项目与性别之间是否存在关系

表2-5 某小学四年级参加课外特长班人数统计表

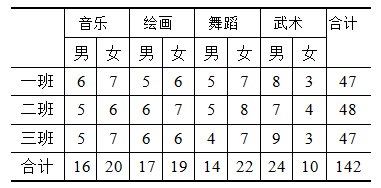
（ 资料来源：X小学教导处）

二、次数分布表

呈现一组连续变量的分布特点，如80名学生的成绩分布，主要是采用次数分布表。即表示数据在各个分组区间内的分布情况，每一个分数区间内包含的观测分数的个数。

次数分布表的结构主要由组别（观测值分组）和次数（频数）构成。下面以80名学生的成绩为例来说明如何制作次数分布表。

表2-6 某校初三80名学生的英语会考成绩统计表

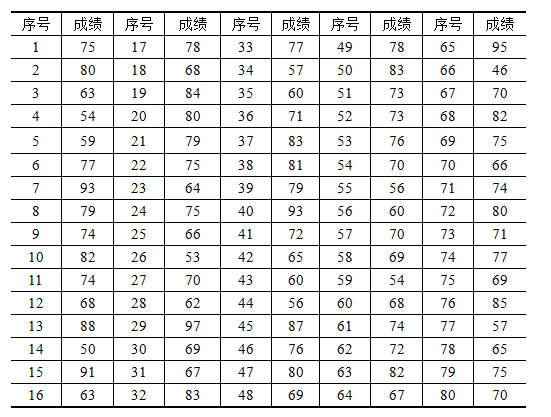
1．求全距。一组观测值中，最大数值与最小数值的差称为全距，用符号表示，即=-。本例=97 ，=46 ，故 ＝97-46＝51（分）。

2．定组数 （分组数目）和组距i。定组数和求全距是编制次数分布表最关键的两个步骤。组数用符号 表示，其确定应考虑数据个数的多少和研究问题的精确度。经验上，分组一般以8～20组为宜。组距是各组数据的组内间距，用符号 表示，常用的组距为2、3、5、10个单位等。组距的大小与组数的多少存在着密切的联系：如果组距过小，组数过多，同质单位的数据就会落在不同组内，组间差异就明显，数据的分布规律却难以显现，由于分组而产生的误差就会增大；如果组距过大，组数过少，会使不同质的单位并在一组，掩盖了组间的差异。本例中组距为5分，组数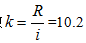，取整数为11。这里要注意，组数的计算结果不能四舍五入，必须保证所分各组能涵盖所有数据。

3．定组限。即各组数据在数值上的起点值和终点值。起点值称为组下限，终点值称为组上限。在确定组限时应注意，第一，次数分布表中最高组区间应包括最大的数据，最低组区间应包括最小的数据；第二，最高组或最低组的下限最好是组距的整数倍；第三，列次数分布表时，各分组区间使用表述组限。本例最低组就写为45~49，上一组为50~54，依此类推……最高组为95~99。这仅是组限的表述形式，其实际代表范围要由组的精确限来确定。如50~54的实际范围是49.5~54.5，并规定 ，其中49.5和54.5分别称组50~54的精确下、上限。

4．求组中值。组中值是居于各组数据分布中点位置的数值，是各组数据的代表值，用符号 表示。组中值的求法是： 。例如45~49一组的组中值 ，或者。其它各组中值求法相同。

5．记录次数。组限确定以后，需将原始观测值按顺序逐一归组，并依次将各组划记的结果记录在相应的组别内，次数用符号 来表示。

6．核对。由于数据在归组过程中容易出现遗漏或重复，应核对总次数，看其是否与数据的总个数相等。这样，组别、组中值和次数构成简单次数分布表，见表2-7。

表2-7 80名学生英语测验成绩次数分布表

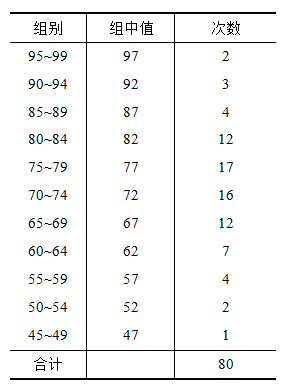
把80名学生成绩绘成这样的统计表后，就能直观地呈现成绩的分布情况，85分以上和55分以下的学生较少，大部分学生成绩在75分左右波动，成绩分布左右较为对称，整体水平不高。

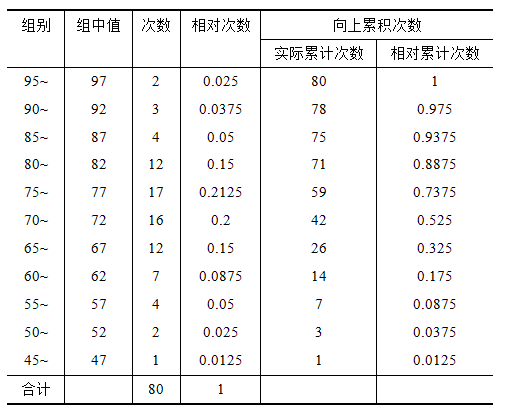
要更直观的呈现某一成绩以上或以下的人数有多少，各分数段人数占整体的比率，可以编制累积次数分布表和相对次数分布表。将次数分布表中各组的实际次数转化为相对次数，即用百分比来表示各组的次数，就编制成相对次数分布表。如由表2-8第一、二、三、四列组成的表就是一个相对次数分布表。通过简单次数分布表中各组对应的次数，进一步求出累积次数，就制成累积次数分布表，如表2-8就是一个累积次数分布表。表中第五、六列为累积次数。表2-8为从下向上累积，即由最低一组开始逐一向上一组累加。通过向上累积次数，可以回答某一分组区间上限以下的次数是多少。如通过表2-8，我们知道有低于69.5分有26人。通过向下累积次数，即从分布表的大数端区间累积次数，可以回答某一分组区间下限以上的次数是多少。在学生成绩分析、成绩比较及教育管理中，常常会用到累积次数分布表，使我们比较方便地了解到某一分组区间上限以下或下限以上的数据总数或数据个数占总体的百分比。

表2-8 80名学生英语测验成绩次数分布表

三、统计表的编制规则

第一，统计表的标题要写在表的上方中央，明确概括出表的基本内容，标明资料所属地区和时间。

第二，统计表要力求简明，避免表内资料过于庞杂；行和列的标目内容要按一定的顺序排列，如果栏目数较多，要加以编号。

第三，统计表中要列出必要的总计数及每一标目以下的小计，以便对数据进行检查和计算；表内数据要填写整齐，对准数位；表中暂缺的数据用“……”表示，根本不存在的数据用“一”表示。

第四，数据资料要注明计量单位，可分别在总标题或行标题、列标题的后面注明。

第五，统计表的上下端线应画粗线，中间各标目内容用细线分开，表的左右两端采取不封闭形式；表格的左上角，一般不绘制斜线，可留空白。

第六，表格内不用文字说明，特殊情况需说明时可用“*”标出，注写于表的下面。资料来源或其他必要的文字说明可写在表的下端。