学以致用是检验学习效果的最好办法，把你们学到的知识在实践中运用一下吧。

实践活动：X中学2010-2011学年第一学期初二期末考试成绩分析报告

实践主题

运用所学集中量数和差异量数对期末考试成绩进行分析。

实践任务

教师首先对其期末考试成绩进行整理，然后根据数据特点将相应的特征量数计算出来，结合实际需要进行数据分析。

参考样例：

X中学2010-2011学年第一学期初二期末考试成绩分析报告

调查对象

调查的具体对象是X中学某班2010-2011学年第一学期初二期末考试成绩分析报告，主要集中在初二年级四个班部分科目成绩和综合成绩的横向和纵向比较，包括及格率、平均分、标准差等。

调查目的

对考试数据进行科学分析的有效手段就是借助专业的描述工具——特征量数。为了全面分析考生的成绩变化，对学生成绩的全面分析至关重要。

考生在接受测验后，按照评分标准对其作答反应直接评出来的分数，叫原始分。原始分反映了考生答对题目的个数，或作答正确的程度。但是，原始分一般不能直接反映出考生的集中水平，考生间差异状况，不能刻划出考生相互比较后所处的地位，也不能说明考生在其他等值测试上应获得什么样的分值。导出分是在原始分的基础上，按一定的规则推导出来的，其目的就是进一步解决原始分所没有解决的问题，或者说，就是为了更好、更科学地解释分数的含义，进行分数的组合，实现分数的等值化。

调查分析

一、微弱优势列第一，四主科齐发力。

本次考试二班总平均分以微弱优势列年级第一。其中语文和英语发挥稳定，保持了一贯的优势，数学较之前有很大提高，物理是学生最喜欢的科目之一，也取得了较好成绩。

二、各科均衡性良好，师生团结攻难关

各科较均衡，从班级角度讲，没有偏科现象。四位主课老师都有很多困难要克服，可是他们对待教学的责任心有目共睹。其中英语相对来讲最“给力”，语文优势不是很明显，主要原因是出现一名“0分作文先生”。数学成绩有很大提高，已经甩掉“软肋”的帽子了。

三、学生个人作战能力强，年级排名显实力

2班有四名学生跻身年级前十名，有八名学生进入前二十名，年级后十名的学生中二班只有一人，27名学生中有18名位于前两个考场，占班级总人数的三分之二。这从整体上能反映出学生的学习积极性较高，水涨船高，学习氛围良好。

四、学习规律不能忽视，一些问题已初露端倪。

1、及格率偏低

相对总平均分第一来讲，及格率偏低，为40.74%，但是低分率也低14.81%，而及格以下，低分以上人数多，为44%。说明本班学生在提高及格率方面有较大空间可以挖掘。下一步工作应该关注中等偏下学生，以提高及格率

2班期末考试及格率和低分率分析

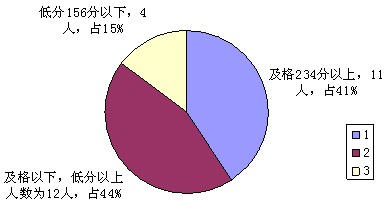
2班期末考试及格率和低分率分析

2、学生两端分化现象已经出现

依据学习规律，初二是学生出现两极分化的开始阶段，在本次考试中也有所体现。从标准差判断，数学的分化程度要大一些。这可能与之前的基础有一定关系，另外就是学科本身的特点决定有小部分学生的学习困难越来越大。其次就是物理，物理作为入门科目，目前分化体现的还不是很明显，但是根据以往经验，这种分化是必然要出现的，因此从现在开始就应该尽力将这种分化的程度降至最低。

2班期末考试各科标准差分析

 

教师分析：

这份实践报告从总体上采用平均数和标准差以及百分比等特征量数描述了数据呈现的状态，分析了考生成绩的集中和离散趋势，并用统计图表来呈现整体分析结果，同时对其原因进行了探究。既结合了本章标准差和平均数等知识点，又把前几章学到的知识点运用其中，做到了学以致用。同时在解释数据时，建议使用更科学、专业的数据语言进行分析。如果本次测试是教师自编测试，对于不同学科的差异程度和一般水平不能直接对比，因为如学生数学成绩与英语成绩是用两个测量工具获得的数据，不是同质数据，这需要对结果进行转换。如果是标准化测试，可以直接比较。再如：

2班期末考试各科标准差分析

从表中可以看出，数学科目的标准差较其他科目更大，语文科目的标准差较其他科目最小，这显示了该阶段数学可能随着难度的加大呈现出偏难和分化的趋势。为了更科学的说明各科成绩的离散程度哪个更大，最好借助差异系数进行分析。