一、集中量数与差异量数的概念

集中量数亦称“数据的中心值”，是描述一组数据集中趋势的量数，它可以概括说明总体某一数量标志的综合特征，反映研究对象在一定时间、地点、 条件下的一般水平。常用的集中量数有算术平均数、中位数、几何平均数等。数据特点不同，使用的集中量不同。

如果只了解数据的集中趋势而忽略其差异情况，可能会做出错误的判断。如某班两个学习小组在一次测验中的成绩，甲组是：50、58、86、87、85、79、98、68、75、84，平均成绩为77分；乙组是65、74、78、80、77、82、75、72、82、85，平均成绩也为77分。两组学生成绩的一般水平一样，但甲组学生成绩的最高分与最低分之差为48分，分布范围较大，而乙组最高分与最低分之差为20分，分布相对集中。因此，对一组数据分布特征的把握，还要了解数据的差异程度。

差异量数是描述一组数据离散程度的量数，有绝对差异量数和相对差异量数两种。绝对差异量数有实际单位，而相对差异量数没有实际单位。全距、标准差、方差、四分差属于绝对差异量数，差异系数是相对差异量数。

差异量数可以衡量集中量数的代表性程度，差异量数愈大，则集中量数的代表性愈小；差异量数愈小，则集中量数的代表性愈大。

二、算术平均数概念及其适用条件

（一）算术平均数的基本概念

算术平均数是指一组同质数据值的总和除以数据总个数所得的商，简称平均数，又叫均值，是用以度量连续变量集中趋势最常用的集中量数。统计学中常用（读谬）表示总体平均数，（读杠）表示样本平均数。设变量代表各次观测的结果，为观测的次数，则

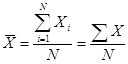
式中 ，为一组数据的算术平均数；

＝【是连加符号，读做西格玛（sigma）】

（二）算术平均数的适用条件

1．适用于同质数据。不同质的数据，不能计算算术平均数。

2．要求一组数据中每个数据都比比较准确、可靠。若数据模糊不清或分组资料有不确定组限时，不能计算算术平均数。

3．无极端值出现。这是由于算术平均数受极端数据影响较大的缘故。

4．需要得到一个相对精确可靠的集中量数或进一步参与其他运算时。

（三）算术平均数的计算方法

对于原始数据，可直接带入公式计算算术平均数。问题导入中32名学生语文成绩的平均分为77.13分，数学平均成绩为75.91分。

问题导入中王老师所教的90名学生的英语成绩已编制成了次数分布表，对于这样已经整理成次数分布表的数据，可根据下面公式来计算算术平均数。

 

式中 ，表示各组的组中值；表示各组对应的次数；表示总次数。

90名学生英语测验成绩次数分布表

解： 。

（四）加权算术平均数的计算

在教育管理中，要考虑各统计事项在其总体中所占的重要性程度。表示统计事项重要性程度大小的量数称为权数。一组同质数据中，每一数值与其对应权数乘积的总和，除以权数之和所得的商，称为加权算术平均数，用符号表示,公式为

   

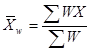
式中， W为每一数值X所对应的权重；为具有不同比重的观测值；

比如《教育统计与测量》这一课程的考核规定，期末成绩由在线作业、实践活动报告和期末成绩合成，所占比例分别为20%、30%和50%。某学生的语文学科这三项的考评成绩分别为90分、87分和92分。该生期末考核成绩就为90.3分。

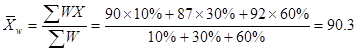
再如某中学初一5个班的代数期中考试成绩如下，该年级的语文平均成绩是多少？

初一代数期中考试成绩统计表

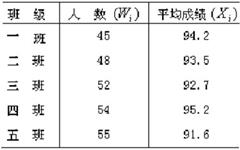
解：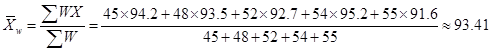

三、算术平均数的性质与优点

平均数的性质	优点	缺点
一组数据中，每一个数值加上（或减去）一个常数后所得到的新的一组数据，其算术平均数等于原一组数据的算术平均数加上（或减去）这个常数。	反应灵敏。观测数据中任何一个数据的变动，平均数都能反应出来。	平均数受极端数据的影响较大。在实际工作中，各种知识比赛、演讲比赛或教师教学比赛等，在计算某一选手的平均得分时，往往是从多个评委的评分中去掉一个最高分和一个最低分，再计算其平均数，就是要避免极端值对平均数的影响，使比赛成绩更客观。
	计算简单。
一组数据中，每一个数值乘上一个常数后所得到的新的一组数据，其算术平均数等于原一组数据的算术平均数乘以这个常数。	确定严密。即严格根据客观数据资料和确定的公式得出的。
	意义简明。平均数概念简单明了，容易理解。
离差平方和为最小。设为任一定值，对于，则有 。	较少受抽样变动的影响。观测样本的大小或个体的变化，对计算平均数影响很小。
	适合于代数运算法则处理。在求解其他统计特征量数时，如方差、标准差，都要应用平均数。