一、中位数的概念及适用情况

在一组有序数据中，居中间位置对应的数据值即为中位数

，用符号表示。中位数可能是一组数据中的某一个，也可能是计算出来的一个数值。由于中位数只取决于位置，在数据众多时，不受极端数值的影响，因此，当一组数据较多，又有极端值，不能用平均数说明集中趋势时，可用中位数作为集中量数的代表值。

中位数的适用情况是：（1）当一组数据有极端值出现时；（2）当一组有序数据两端有个别数据模糊不清或分组资料有不确定组限（最上限，最下限）时；（3）当需要快速估计一组数据的代表值时。

二、中位数的计算方法

    （一）

未分组数据中计算中位数

 

问题导入中32名学生语文成绩的中位数为：

排序后中间位置序号为，说明中间数在第16位和第17位之间，所以中位数是第16位与第17位对应数据值和的一半，即。与平均数有一定差异，这是因为中位数是通过位置来确定，不是每一个观测值都参与运算，因此，误差比较大。

（二）次数分布表数据计算中位数

如果一组数据已列成了次数分布表，则处在50%这点上的数值就是中位数。自下向上累积时计算公式为：

式中，表示中位数；表示中位数所在组的精确下限；

表示中位数所在组下限以下的累积次数；表示中位数所在组对应的次数；

表示组距；为总次数

如下面是某小学四年级55名学生英语成绩的次数分布，请确定其中位数。

解： ①确定中位数位置及其所在组。中位数的位置为，由向下向上累积次数大于或等于的这一组为中位数所在组，可知中位数所在组为50~54这一组，如图中两虚线之间的分数段。

②赋值。，=10，=25，=5，=55。

③代入公式

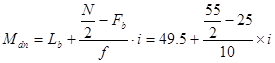=50.75

（三）中位数的优缺点

从中位数的计算来看，中位数的优点表现为：严格根据客观数据资料和确定的公式得出，不是主观臆定的；计算简单，意义简明，容易理解和掌握；不受极端数值的影响等。但中位数是居中的量数，并非每个数据都参与计算，因此，其大小不受制于全体数据；反应不够灵敏；没有算术平均数可靠；易受抽样偏差的影响，不如平均数稳定；不能作进一步的代数运算。