一、几何平均数的概念和适用情况

在教师评价工作中，通常要考察学生的学习效果，仅凭一、两次考试成绩的高低作出判断，往往不能令人服气。为此，要考虑如何利用提高率来衡量其进步或退步情况。在教育科研与教育管理活动中，统计学习次数与能力提高的关系，计算提高(或下降)率、经费提高的比率、学校经费增加率、教师工资增加率、教育发展水平预测等均可使用几何平均数。

几何平均数是个数值连乘积的次方根，用符号表示，即。注意：X是指后一个数是前一个数据的倍数；N是后一个数是前一个数倍数的个数。

如果一组数据值按比例递增或递减（一个数列的后一个数据是以前一个数据为基础成比率增长
），表示其平均水平时应使用几何平均数，常用于表示某现象的平均发展速度、平均增长率等。

二、运用几何平均数求平均发展速度和进行教育预测

教育现象的发展常表现出时快时慢的动态特征。为了掌握其发展规律，了解它在各个发展阶段增减变化的一般速度，就需要计算平均发展速度和平均增长率等指标。它不但可以反映教育现象发展的一般规律，而且对教育发展的长期规划、监督检查计划的执行情况、估计预测某种数量，都是不可缺少的辅助手段，如教育的发展与教育经费的有计划分配，在校生人数的增减与办学规模的合理控制等等。

平均发展速度是各阶段发展速度的平均值。下面以问题中所提到的分析1997-2007年普通小学全国生均预算内教育事业费的发展速度为例，说明如何计算几何平均数。

设为各阶段某种统计量值，其中为初期量、为末期量，为各阶段环比发展速度。即。的几何平均数便是平均发展速度。即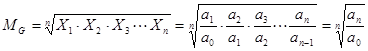 

根据平均发展速度可计算平均增长率，并依此对某种教育现象进行预测。用表示平均增长率，则=-1， 

依据公式求得1997-2007年普通小学全国生均预算内教育事业费的发展速度为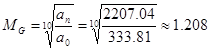，平均增长率为1.208-1=20.8%。按照这样的速度发展，到2017年普通小学全国生均预算内教育事业费会达到：元。