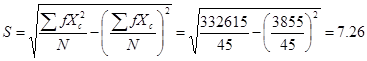一、全距

全距又叫极差，是指一组观测值中，最大数值与最小数值之差，用符号表示，即。它是描述一组观测值离散程度最简单的一种差异量数，如问题导入中32名学生语文成绩的全距为分。
对于次数分布表，最高组的精确上限与最低组的精确下限之差即为全距。如问题导入中90名学生英语成绩的全距为99.5-49.5=50分。

全距是最简单、最易理解的差异量数，但它只是一组数据分散程度粗略的度量值，取决两个极端数据，不能反映其他数据的分散情况，是一种低效的差异量数。如何才能反映全体数据的差异情况呢？标准差能帮我们解决这一问题。

二、方差与标准差的概念与适用情况

（一）方差与标准差的概念

标准差是从方差演变而来的。方差是一组数据离差平方和的平均数，也叫变异数。方差的算术平方根称为标准差。方差和标准差是最常用的描述数据分布离散程度的差异量数，反映了各变量值与均值的平均差异。总体方差用符号（读西格玛，sigma）表示，样本方差用符号表示。定义公式分别为：和 

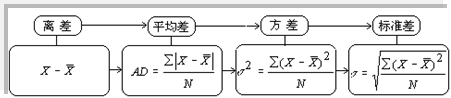
总体标准差用符号表示，样本标准差用S表示。公式为

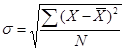和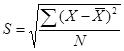

式中，为原始观测值；为平均数

为了计算方便，可直接使用原始观测值计算标准差，公式为：

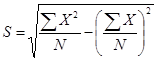
式中，为标准差，为原始观测值，为观测值个数

用原始数据计算标准差，充分利用了每一个原始观测值来计算标准差，精确度很高，同时不需要先求出平均数，计算更简单。

（二）标准差的性质及适用条件

标准差的性质主要有两点：第一，每个观测值都加上或减去一个相同的不为零的常数C，所得标准差等于原标准差。第二，每个观测值都乘以一个相同的常数C，所得的标准差等于原标准差乘以C。（注：C不为零）

标准差的适用条件主要有：（1）一组数据的一般水平适合算术平均数描述时，其离散程度宜用标准差来描述。（2）进一步参与其他运算时。如计算差异系数、相关系数等其他统计量。（3）在推断统计，尤其在方差分析时，常用方差表示数据的离散程度。

三、标准差的计算

（一）对未分组数据计算标准差

问题导入中李老师所抽取的32名学生的语文和数学成绩是未分组数据，其标准差计算采用公

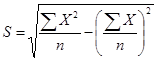，将数据带入公式求得分，分。

（二）次数分布表计算标准差

分组资料求标准差，同分组资料求平均数一样，用组中值做为各组数据的代表值，计算公式为：

 

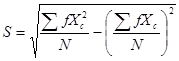
式中，表示组中值，表示各组对应的次数，为总次数。

如某班45名学生的语文成绩如下表，求分析这45名学生成绩的差异情况。

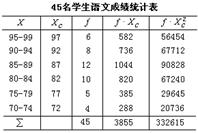
解：将上述表中计算的中间结果代入公式得：