一、随机事件

问题导入中在320名学生中随机抽取一名学生，可能是男生，也可能是女生；64名学生的成绩有高有低，等等。像这样的现象是随机现象。概率论是从量的方面研究随机现象的统计规律的科学。随机现象中出现的各种可能的结果，叫做随机事件，简称事件。常用大写字母A、B、C……表示。如随机抽取的 64名学生，结果可能是没有不及格，可能是有一个不及格，也可能是有两个不及格，或者不及格数不多于4等等。其中每一个结果都是一个事件。“没有不及格”、“有一个不及格”、“有两个不及格”等叫做基本事件（不能分解为其他事件的最简单事件）；而不及格数不多于4个等叫做复合事件（由若干个基本事件复合而成）。一般来说，在试验条件下必然发生的结果叫做必然事件，不可能发生的结果叫做不可能事件。

二、事件的概率

（一）频率

在抽取的64名学生中，女生30名，抽取学生为女生这一事件的频率就是30/64。所以对于随机事件A，如果在N次试验中出现次，则A发生的频率为：    

（二）经验概率

某事件在试验中发生的次数与试验总次数的比值为频率。试验次数越多，该事件发生的频率会在某个常数上下波动，当试验次数无穷时该事件发生的频率会与这个常数相等，这个常数称为该事件的概率。

一个事件的频率是变量。这是因为在n次试验中，事件A发生的次数不是一个固定的常数，它可以随机地取0、1、2、……n中的任何一个值。但多次试验，会发现频率具有稳定性。历次统计学家抛掷硬币正面向上的试验结果可以说明这一点。

历次统计学家抛掷硬币的试验结果

（三）先验概率

也称古典概率。如果试验满足各种可能结果（基本事件）是有限的、各种可能结果发生的可能性不变这两个条件，则称此试验为古典型试验。设试验的一切基本事件有N个，而事件A所包含的基本事件有K个，则事件A的概率定义为：

         

如“问题导入”中随机抽取一名学生为女生的概率为150/320。

（四）概率的性质

频率是大量试验的结果，是一个随试验次数变化而变化的数值，是事件发生的外在表现，是一个变量；概率是一个确定值，体现了事件发生的内在实质，是一个常量。概率的性质有以下三条：

（1）对于任何事件A，总有0≤≤1。

（2）若U为必然事件，则＝1 。

（3）若V为不可能事件，则＝0 。

（五）小概率事件

如果某一事件发生的概率很小，即在多次重复试验的情况下，发生的概率小于或等于0.05，则称其为小概率事件。比如买彩票中大奖就是一个小概率事件。小概率事件在一次试验中几乎不可能发生，这是在统计推断时所依据的基本原理。

三、概率的两个法则

（一）概率的加法法则

事件A和事件B是两个互不相容的随机事件，则事件A与事件B之和的概率等于这两个事件分别发生的概率的和，即

(A＋B)＝P(A)＋P(B) 

互不相容事件是指事件A与事件B不可能在一次试验中同时发生。如做一道是非判断题，要么做对，要么做错。两事件和的概率是指两事件中有一个发生，则第三件事（A＋B）发生的概率（A发生或B发生）。

如某幼儿园中班有122名幼儿，其中朝鲜族幼儿10人，回族6人，蒙族3人，其余是汉族学生，若从中班幼儿中随机抽取一个孩子，问抽到少数民族的孩子的概率是多少？

解：设A、B、C分别表示朝鲜族、回族和蒙族孩子三个事件，而A＋B＋C则表示少数民族孩子这一事件，在122名孩子中随机抽取一个孩子恰是少数民族学生的概率是

(A＋B＋C)＝(A)＋P(B)＋(C)==0.156

注意互不相容事件和对立事件的区别。两个互不相容事件的概率之和不一定为1，而两个对立事件的概率之和必然等于1，对立事件是互不相容事件的一种特殊情况。

（二）概率的乘法法则

若事件A和事件B相互独立，则这两个事件之积的概率等于这两个事件分别发生的概率之积，即P（A·B）＝P（A）·P（B）

相互独立事件是指其中任何一个事件发生与否，都不影响另一个事件发生的可能性。而两个事件之积的概率是两个事件分别发生的概率的积。如凭猜测做两道是非判断题，第一题猜对与否和第二题没有关系。第一题猜对且第二题也猜对的概率即是两道题猜对的概率之积。

如某校二年级共有学生90人，其中一班有学生48人，二班有学生42人，在一次语文考试中，共有70人在80分以上。假如两班学生学习成绩是均衡的，那么从全年级随机抽取1名得80分以上且是二班学生的概率是多少？

解：设A和B分别表示80分以上和二班这两个事件，由于A和B是独立的，因此这个问题的解决符合概率的乘法法则。随机抽取一个学生，抽到80分以上而且是二班学生的概率就是A、B两个事件同时发生的概率P（A·B），由于

P（A）＝，P（B）＝

所以P（A·B）＝P（A）·P（B）

从全年级随机抽取1名学生，抽得80分以上而且是二班学生的概率是0.36。

四、二项分布的概念

二项分布是二项试验中各种可能结果的概率分布，是教育研究与管理中常用的一种离散型随机变量的概率分布。

（一）二项试验

凡满足下列条件的试验称为二项试验：（1）任何一次试验的结果只有两种可能，即成功或失败，如判断正误题、选择题等；（2）若成功的概率为 p，失败的概率为 q，则 p+q=1；（3）每次试验中成功或失败的概率不变，即成功的概率在第一次试验中为p，则在n次试验中的概率都是p；（4）各次试验结果相互独立。

（二）二项分布

二项分布是指在二项试验中，如果n次试验中事件A可能出现的次数k（k=0，1，…，n）是随机的，也就是n +1个概率值，则事件A出现各种可能结果的概率分布。二项分布中事件A出现k次及其概率与二项展开式的各项相对应。

当学生完全凭猜测回答两道是非题时，其可能结果有三种：全猜对、一对一错、全猜错。若猜对事件为A，猜错事件为B，则

全猜对的概率为：

一对一错的概率：

全错的概率为：

而，即

当学生凭猜测回答三道是非题时，可能结果有四类：全猜对、猜对两道错一道、猜对一道错两道、全猜错，共八种可能情况，各种情况的概率为：、、、、、 、、。这八种情况的概率分布如下图所示：

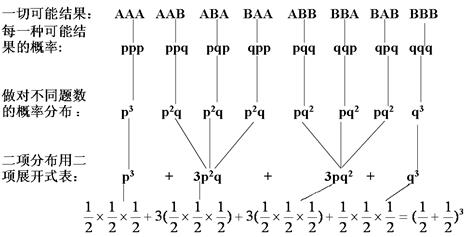
由上图可知，学生做三道是非题，做对不同题目数量的概率分布可以用三次二项式的展开式来表达。同样可推知，当学生做四道是非题时，做对不同题目数量的概率之和可表示为：

由此可见，二项试验的各种可能结果出现的概率，恰是二项展开式各项的值，试验的次数就是二项式的指数。二项展开式的一般形式是：

 

展开式中任何一项 表示在n次试验中某事件发生 k次的概率，而系数表示在所有可能结果中，这种结果出现的次数为。因此，

在n次试验中某事件发生k 次的概率可概括为一个通式：

（k=0，1，2，…，n）

这个通式叫二项分布函数式，运用这一函数式可以直接求出n次试验中A事件出现k次的概率。

某中学生凭猜测做7道是非题，问7道题中答对2道、3道、4道的概率各是多少？

解：本题试验次数为n=7，做对的概率p =，做错的概率q=，则试验7次，做对2道的概率为：

7道题中答对3道的概率是：

五、二项分布的平均数和标准差

二项分布的平均数，是指二项分布中随机变量k的算术平均数，实质上它是以k为原始数据，以概率p(成功事件)为权数的加权算术平均数。二项分布的平均数为

           

二项分布的标准差，是指二项分布中随机变量k的标准差（成功次数的离散程度）。二项分布的标准差为

         

六、二项分布的应用

利用二项分布可以估计带有机遇性的实际问题。

如英语考试共有20道选择题，均为四选一题。规定每题答对得1分，答错或不答得0分。有一个学生说他过去没有学过英语，全凭猜测答题，问：

（1）凭猜测，他得18分以上的概率是多少？

（2）答对多少道题可以认为他不是猜的？

解：做答20道选择题，可以看成是做20次试验。每次试验只有两个结果，每题猜对的概率为，猜错的概率为。

（1）求该学生凭猜测得18分以上的概率，实际上是求他得18分或者19或者20分的概率是多少，即三种获得分数的概率之和： 

此概率非常小，说明完全凭猜测想得高分是不可能的。

（2）判断该学生答对多少道题可以认为他不是猜的，只需知道他答对多少题时属于小概率事件，则可判定他答对该题数时就认为不是猜的。由于本题,答题的各种可能结果近似服从正态分布，因此可依据正态分布理论解决此问题。当答题得分为Z＝1.64时，P=0.05，属于小概率事件,此时，已知，，

所以

＝

即当该学生答对9道题时，可以认为他不是猜的。