第四章 概率分布与参数估计
 知识点二:正态分布
知识点二:正态分布
人的能力水平、学生学业成绩、家庭经济收入水平等很多现象都呈现中间多、两头少的分布状态,像这样的中间频数多、两头频数对称地减少,成一个“钟”形对称的分布称为正态分布,它是一种最常见、用处最广的理论上的连续变量的概率分布。正态分布是许多统计方法的前提条件。
一、一般正态曲线
正态分布曲线是一种均匀的圆滑曲线,其方程为:
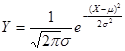
式中,![]() 是正态曲线的高度,表示某观测值出现的相对次数;
是正态曲线的高度,表示某观测值出现的相对次数;![]() 是变量观测值,可能取值(-∞,+∞);
是变量观测值,可能取值(-∞,+∞);
![]() 是观测值总体的平均数;
是观测值总体的平均数; ![]() 是观测值总体的标准差;
是观测值总体的标准差;![]() =3.14(圆周率) ;
=3.14(圆周率) ;![]() =2.7183(自然对数之底)。
=2.7183(自然对数之底)。
从方程看出,正态曲线是关于![]() =
=![]() 这一点的纵线为对称轴的轴对称图形(对称图形不一定是正态分布)。
这一点的纵线为对称轴的轴对称图形(对称图形不一定是正态分布)。![]() 和
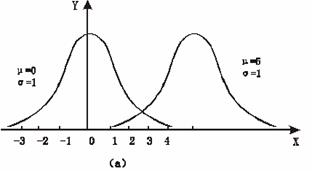
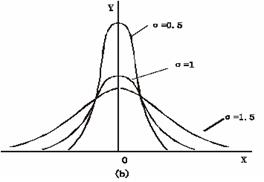
和![]() 称为正态分布的两个参数,正态分布曲线的位置和形状随其总体的平均数和标准差的不同而变化。平均数不同,曲线在横轴上的位置就不同,如图(a);标准差不同,则曲线的高矮及与底线距离的长短不同,如图(b)。当标准差较大时,观测值分散在较大范围内,
称为正态分布的两个参数,正态分布曲线的位置和形状随其总体的平均数和标准差的不同而变化。平均数不同,曲线在横轴上的位置就不同,如图(a);标准差不同,则曲线的高矮及与底线距离的长短不同,如图(b)。当标准差较大时,观测值分散在较大范围内,![]() 的最大值较小,正态分布曲线形状较平缓;相反,观测值分散在较小范围内,
的最大值较小,正态分布曲线形状较平缓;相反,观测值分散在较小范围内,![]() 的最大值较大,正态分布曲线形状较陡峭。因此,在同一坐标系中可以画出无数条平均数不同、标准差不同的正态分布曲线。所以,正态分布曲线是一簇曲线。
的最大值较大,正态分布曲线形状较陡峭。因此,在同一坐标系中可以画出无数条平均数不同、标准差不同的正态分布曲线。所以,正态分布曲线是一簇曲线。
二、标准正态分布曲线
在无数条正态分布曲线中有一条平均数为0、标准差为1的曲线,这条曲线称为标准正态分布曲线。其曲线方程为:
![]()
标准正态分布曲线只有一条,它是一种固定形态的正态分布。如果原始随机变量的取值服从正态分布,那么其标准分数的平均数为0,标准差为1,则这组标准分数就服从标准正态分布。
标准正态分布曲线的特点:
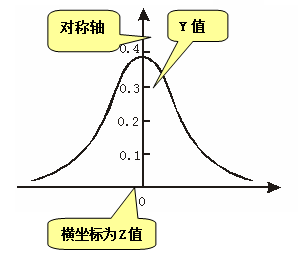 1.曲线最高点为
1.曲线最高点为![]() =0,
=0,![]() =0.3989,标准正态分布曲线在
=0.3989,标准正态分布曲线在![]() =0处
=0处![]() 值最大。曲线下的总面积即概率的总和为1,对称轴左右各0.5。
值最大。曲线下的总面积即概率的总和为1,对称轴左右各0.5。
2.曲线是以过![]() =0的纵线为对称轴、呈钟形的轴对称图形,曲线两侧横坐标绝对值相等的对应点的高度相等,对应的曲线下面积相等。
=0的纵线为对称轴、呈钟形的轴对称图形,曲线两侧横坐标绝对值相等的对应点的高度相等,对应的曲线下面积相等。
3.标准正态分布的平均数、中位数、众数都在![]() =0这一点,而且多数观测值集中在这点附近。
=0这一点,而且多数观测值集中在这点附近。
4.曲线与对称轴交点处(即![]() =0处)
=0处)![]() 值(相对次数)最大,概率最大。曲线从最高点向两侧先快后慢对称下降,在
值(相对次数)最大,概率最大。曲线从最高点向两侧先快后慢对称下降,在![]() =+1处有两个拐点,几乎包括观测值总数的2/3;左右各3个标准差范围内基本包括全部观测值;横轴是标准正态分布曲线的水平渐进线,曲线向两侧逐渐接近横轴,但永远不与横轴相交,所以
=+1处有两个拐点,几乎包括观测值总数的2/3;左右各3个标准差范围内基本包括全部观测值;横轴是标准正态分布曲线的水平渐进线,曲线向两侧逐渐接近横轴,但永远不与横轴相交,所以![]() 值永远不会等于零。
值永远不会等于零。
三、标准正态曲线下的面积及正态分布表的使用
什么是正态曲线下的面积?其意义是什么?正态曲线与其底边所围成的面积称为正态曲线下的面积,代表数据分布的总次数,即概率之和。正态曲线与基线之间某一区间的面积,相当于在该区间找到某个个体的概率。曲线被对称分为两部分,两部分面积各占总面积的一半,即概率之和为50%。
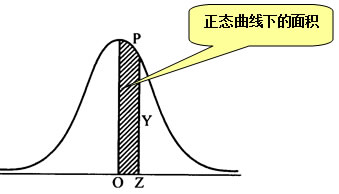
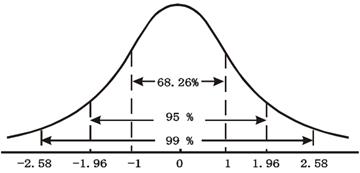
标准正态曲线下的总面积为1,各部分的面积比率是确定的,如下图所示。在![]() =0左右各一个标准差的范围内,包括总面积的68.26%[表中
=0左右各一个标准差的范围内,包括总面积的68.26%[表中![]() =-1与
=-1与![]() =1两点的纵线所夹的图形的面积比率,表示相应区间内随机变量的概率],左右1.96个标准差之间,包含总面积约95%,左右2.58个标准差之间,包含总面积约99%。标准正态曲线下的各种
=1两点的纵线所夹的图形的面积比率,表示相应区间内随机变量的概率],左右1.96个标准差之间,包含总面积约95%,左右2.58个标准差之间,包含总面积约99%。标准正态曲线下的各种![]() 值对应的面积比率及
值对应的面积比率及![]() 值都可以由从正态分布表直接查出。
值都可以由从正态分布表直接查出。
在正态分布表中,列出与各种![]() 值对应的曲线高度
值对应的曲线高度![]() 和
和![]() =0至某个
=0至某个![]() 值间的面积比率
值间的面积比率![]() 。因为正态曲线下
。因为正态曲线下![]() =0处左右对称,所以表中仅列出了
=0处左右对称,所以表中仅列出了![]() =0右侧的
=0右侧的![]() ,
,![]() ,
,![]() 值。利用正态曲线下的面积,已知
值。利用正态曲线下的面积,已知![]() 值,可求与之对应的
值,可求与之对应的![]() 值,或是已知
值,或是已知![]() 值,求
值,求![]() 值。
值。
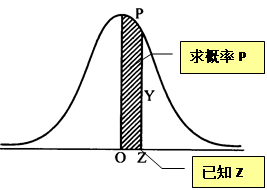 1.已知
1.已知![]() 值,求面积P
值,求面积P
利用正态分布表,求
(1)![]() =0至
=0至![]() =1之间的面积比率;
=1之间的面积比率;
(2)![]() =1.96以上和
=1.96以上和![]() =-1.96以下的面积比率;
=-1.96以下的面积比率;
(3)![]() =1.64左侧的面积比率
=1.64左侧的面积比率
解:查正态分布表,可得:
(1)![]() =1时,
=1时,![]() =0.34134,所以
=0.34134,所以![]() =0至
=0至![]() =1之间的面积比率为0.34134;
=1之间的面积比率为0.34134;
(2)![]() =1.96以上的面积等于0.5减去
=1.96以上的面积等于0.5减去![]() =0至
=0至![]() =1.96之间的面积,
=1.96之间的面积,![]() =0至
=0至![]() =1.96的面积比率为0.475,所以
=1.96的面积比率为0.475,所以![]() =1.96以上面积比率为0.5-0.475=0.025;
=1.96以上面积比率为0.5-0.475=0.025;![]() =-1.96以下面积与
=-1.96以下面积与![]() =1.96以上面积部位对称,因此
=1.96以上面积部位对称,因此![]() =-1.96以下的面积比率亦为0.025。
=-1.96以下的面积比率亦为0.025。
(3)![]() =1.64时,对应的
=1.64时,对应的![]() =0.44950,求其左侧的面积就是曲线左半部分的面积比率与
=0.44950,求其左侧的面积就是曲线左半部分的面积比率与![]() =0到
=0到![]() =1.64之间的面积之和,即:0.5+0.44950=0.94950。
=1.64之间的面积之和,即:0.5+0.44950=0.94950。
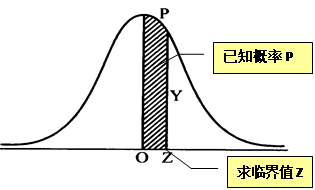
2.已知![]() 值求
值求![]() 值
值
利用正态分布表求:
(1)正态曲线下右尾和左尾面积各为0.05对应的![]() 值;
值;
(2)正态曲线下中间面积0.95比率上下界限对应的![]() 值。
值。
解:查正态分布表可得:
(1)正态曲线下右尾0.05面积比率对应的![]() 值即是面积0.45对应的
值即是面积0.45对应的![]() 值。从正态分布表中
值。从正态分布表中![]() 值一列找不到0.45这个值,则找到0.45最接近的0.4495,它对应的
值一列找不到0.45这个值,则找到0.45最接近的0.4495,它对应的![]() =1.64,便是所求;由于左尾和右尾概率相同,所以左尾0.05面积比率对应的
=1.64,便是所求;由于左尾和右尾概率相同,所以左尾0.05面积比率对应的![]() 值为-1.64。
值为-1.64。
(2)正态分布中间0.95的面积比率在![]() =0处被平分,而且上下界限对应的
=0处被平分,而且上下界限对应的![]() 值对称,
值对称,![]() ,即当P=0.475时,查其对应的Z,Z=1.96,即中间0.95面积比率上下界限对应的
,即当P=0.475时,查其对应的Z,Z=1.96,即中间0.95面积比率上下界限对应的![]() 值为
值为![]() ;同理
;同理![]() ,从正态分布表中找到与0.495最接近的值0.49506,其对应的
,从正态分布表中找到与0.495最接近的值0.49506,其对应的![]() =2.58,所以中间0.99面积比率上下界限对应的
=2.58,所以中间0.99面积比率上下界限对应的![]() 值为
值为![]() 。
。
四、正态曲线下面积的利用
(一)推求考试成绩中特定区间的人数
某市600名小学生的数学竞赛成绩服从正态分布,其平均成绩为65分,标准差为15分,利用正态分布曲线下的面积推求60分以下,60—70分,70—80分,80分以上各段可能占总人数多大比例?并估计各分数段各有多少人?
解:由于600名学生的数学成绩服从正态分布,因此可根据正态分布曲线下的面积推求各段人数。
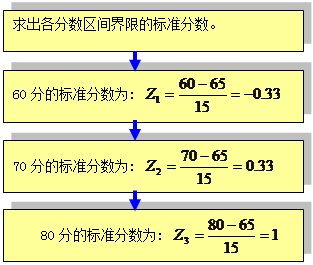
然后查正态分布表中![]() 值对应的面积比例
值对应的面积比例![]() 。
。
当![]() =0.33时,查表得
=0.33时,查表得![]() =0.12930;
=0.12930;
当![]() =1时,查表得
=1时,查表得![]() =0.34134;
=0.34134;
利用正态曲线的对称性知60分以下的人数比例为0.5-0.12930=0.3707,60—70分的人数比例为0.12930×2=0.2586,70—80分的人数比例为0.34134-0.12930=0.21204,80分以上的人数比例为0.5-0.34134=0.15866。
最后用总人数乘以各分数段人数比例,求得各分数段的可能人数。由于参加考试的人数有600人,所以各分数段的人数(以整数计)为:
60分以下:![]()
60—70分:![]()
70—80分:![]()
80分以上:![]()
各分数段人数之和应等于参加考试的总人数,即223+155+127+95=600。
(二)推求考试成绩中某一特定人数比率的分数界限
如600名小学生数学成绩服从正态分布,平均成绩65分,标准差15分,如果计划选取出120名参加省里竞赛,那么选取的分数线最底应是多少?
解:将选取的人数比率作为正态分布曲线右尾部面积比率,在正态分布中找出与之对应的标准分数![]() 值,然后根据
值,然后根据![]() 值用公式
值用公式![]() ,求出原始分数
,求出原始分数![]() 的值。
的值。
选取比率为:![]()
按面积比率0.5-0.2=0.3,查正态分布表,找到与0.3最接近的0.29955对应的![]() =0.84,所以录取分数估计是:
=0.84,所以录取分数估计是:![]() 。
。
(三)确定按能力或成绩等级分组的各组人数
若对500名学生的写作能力按优秀、良好、中等、及格、不及格五级评定,已知学生写作能力服从正态分布,用正态曲线下的面积推测一下各等级应该有多少人?
解:由于正态分布情况下,![]() 之间几乎包括了全部观测值,因此可认为500名学生的写作能力等级分布在
之间几乎包括了全部观测值,因此可认为500名学生的写作能力等级分布在![]() 的范围内;又由于各等级间距离相等,因此可以把
的范围内;又由于各等级间距离相等,因此可以把![]() 区间平均分成五等份,即每一等级占的区间长为
区间平均分成五等份,即每一等级占的区间长为 ![]() 。
。
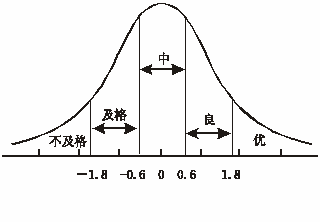
图中显示出优、良、中、及格、不及格各等级的![]() 分数区间,查正态分布表,求得各等级人数比例分别为:
分数区间,查正态分布表,求得各等级人数比例分别为:
优:0.5-0.46407=0.03593,即![]() =1.8右侧对应的面积比例。
=1.8右侧对应的面积比例。
良:0.46407-0.22575=0.23832,即![]() =0.6与Z=1.8之间的面积比例。
=0.6与Z=1.8之间的面积比例。
中:0.22575+0.22575=0.4515, 即![]() 之间的面积比例。
之间的面积比例。
及格:![]() =-1.8与
=-1.8与![]() =-0.6之间的面积比例,它与
=-0.6之间的面积比例,它与![]() =0.6到Z=1.8之间的面积对称,所以也是0.23832。
=0.6到Z=1.8之间的面积对称,所以也是0.23832。
不及格:即![]() =-1.8左侧的面积比例,与
=-1.8左侧的面积比例,与![]() =1.8右侧的面积对称,即0.03593。
=1.8右侧的面积对称,即0.03593。
用被评定的总人数N=500分别乘以各等级的人数比例,便求得各等级的相应人数,即
优秀和不及格的人数都是500×0.03593=18
良好和及格的人数都是500×0.23832=119
中等的人数为500×0.4515=226
各等级人数之和应等于总人数,即:18×2+119×2+226=500
注意:如果各等级人数之和与已知总人数不等时,将居中的那一组做适当的减少或增加。
