某乡中心小学调查小学一年级学生的体重情况，该乡小学一年级有学生3500名，如果把该乡小学一年级学生的体重作为一个总体，那么这3500名学生的体重测量值的频数分布就是一个总体分布；如果在其中随机抽取85个体重测量值，则这85个数值的频数分布就是一个样本分布。因此，总体分布、样本分布都是实际观测值的分布。如果将所抽的85个体

重测量值（样本容量n），分别求出其平均数和标准差后再放回总体中，然后再随机抽出85个测量值，求平均数、标准差。反复这一过程我们就得到样本容量为n=85的所有可能个样本的平均数和标准差。这些所有可能个样本平均数和标准差不会都相同，这些所有可能个样本的平均数的分布称为平均数的抽样分布；这些所有可能个样本标准差的分布称为标准差的抽样分布。

一、抽样分布的基本概念

（一）抽样分布的概念

抽样分布是指某种样本统计量的概率分布。即把某种样本统计量看作一个随机变量，从总体中抽出相同容量的全部可能样本，计算出统计量的值，这个统计量的全部可能值构成的新的总体所形成的分布就是抽样分布。

每一种统计量的抽样分布，都有它自己的形态特点，也有它独特的分布参数值。研究抽样分布就是要确定不同条件下形成的抽样分布各是什么形态，它们的分布参数如平均数、标准差等分别是多大。如果我们掌握这些样本统计量的概率分布规律特点，就可以依据样本统计量的特征，采用恰当的统计方法，实现对总体特征的推断。因此，抽样分布是统计推断理论的依据。

（二）抽样分布的平均数与标准误

抽样分布也有描述其分布特征的统计指标。用平均数来描述抽样分布的集中趋势，称为抽样分布的平均数；用标准差来描述抽样分布的离散程度，为了与总体标准差和样本标准差区别开来，称之为标准误，用SE表示。如样本平均数抽样分布的标准差称为平均数的标准误，符号为。不同的统计量，标准误计算方法不同。标准误用符号SE表示。标准误是推断统计中的一个重要指标。标准误越小，表明样本统计量与总体参数间的差异。标准误越小，样本对总体的代表性越强，用样本统计量推断总体参数可靠性越强。

（三）自由度

在统计推断中，尤其是小样本的统计方法中都涉及确定自由度的问题。对于任一随机变量的取值变化，在总体上，它是无任何限制的，每个随机变量的取值都是自由变化的，其自由度也是无限的。但是在有限样本中，统计量的计算往往受到一定的限制，会失掉一定自由度。例如从某一总体N个随机变量中随机抽取n个数值，则这n个数值构成一个样本。当我们求这n个数值的方差时，就会失掉一个自由度。这是因为当样本值给定后，n个数值的和就确定了，样本平均数也就确定了。这样，n个数中，前n-1个数据都可以自由取值，而第n个数会受到全部数据的平均数的制约而不能自由取值，要由公式求得。在求方差时，式是n个离差平方之和。但这n个的量不能自由变化，要受到这一条件的约束，所以样本方差的自由度是n-1。自由度失去的多少取决于计算统计量时实际受约束条件的多少，例如在总体平均数差异的t检验中，计算标准误只受的限制，自由度是n-1；而在两个样本平均数差异的t检验中，计算标准误受到和两个因素的限制，因此，自由度是n1+n2-2。在假设检验中，自由度根据不同情况取不同的值。

二、样本平均数的抽样分布

在各种统计量的抽样分布中，样本平均数的抽样分布最典型，用得也最多，这里以平均数的抽样分布为例阐述抽样分布的基本理论。

统计上已证明，样本平均数是以总体平均数为中心而分布的。即平均数抽样分布的平均数为总体平均数。

标准误为：

式中，为总体标准差；为样本容量

此式表明，平均数的标准误与总体标准差成正比，与样本容量的平方根成反比。当总体标准差已知时，样本容量越大，平均数的标准误就越小；当样本容量n一定时，总体内个体数值的离散程度越小，平均数的标准误越小。标准误越小，表明样本统计量与总体参数的值越接近，样本对总体越具有代表性，用样本统计量推断总体参数的可靠性越大。因此，标准误是统计推断可靠性的指标。

（一）总体正态分布，总体方差已知

此时无论样本容量大小，样本平均数抽样分布的标准误。

（二）总体正态分布，总体方差未知

大样本时，样本平均数的抽样分布为正态分布，标准误。

小样本时，服从自由度为n-1的t分布。此时，样本平均数抽样分布的标准误为：

式中，；；为样本容量。

1.t分布

t分布是统计分析中应用较多的一种抽样分布，这种分布是一种左右对称、峰态比较高狭、分布形状随自由度的变化而变化的分布。

t分布与标准正态分布相似之处，一是平均值为0；二是以平均值0左右单峰对称分布；三是取值范围为-∞到+∞；四是曲线以平均数处为最高，向两侧逐渐下降，尾部无限延伸，但永不与基线相交，如图4.7所示。

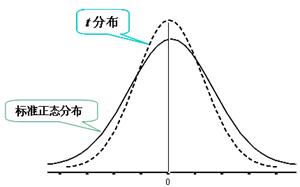
t分布曲线与标准正态分布曲线

与标准正态分布不同的是，t分布曲线不是一条，而是一簇，随着自由度的不同而得到不同的曲线。自由度越小，t分布曲线越矮平，尾部翘得越高，与标准正态分布曲线差异越大；自由度越大，t分布曲线与标准正态分布曲线越接近；当自由度接近无穷大时，t曲线与标准正态分布曲线重合。

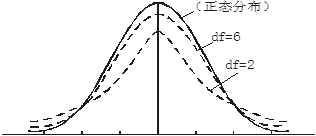
t分布与标准正态分布的关系

2．t分布表

在依据t分布理论进行统计推断时要查t分布表。附表2是常用的t分布表，是利用t变量的分布函数，根据自由度和显著性水平不同而计算的t变量的临界值。t分布由三方面数值构成，即t值、自由度和显著性水平。表的左列为自由度，最上一行是不同自由度下的t分布两尾端的概率，即双尾检验的显著性水平，最下一行是单尾检验的显著性水平。只要给出自由度和显著性水平，利用t分布表就可以查到临界值，使用方便。如=18，=0.05，双尾检验时查得=2.101，这意味着t值小于-2.101的概率与t值大于2.101的概率之和为0.05。同时，通过t分布表，我们可以看出，相同显著性水平下，t值随自由度变化而不断发生变化，当接近无穷大时，t值与Z值相同。

（三）总体非正态分布，但样本容量n≥30

在大样本（n>30）时，尽管总体非正态分布，其样本平均数的抽样分布形态与正态分布形态的差异已经非常小，样本越大，这种差异越小，其间的差异，不足以对我们的进一步分析产生影响。因此，在大样本情况下，无论总体是否正态分布，可以认为平均数的抽样分布为近似服从正态，可以用公式，求平均数的标准误。在教育研究上，比较容易取得大样本，因此教育研究中经常依据正态分布理论，采用大样本的研究方法。