一、区间估计的界定

以样本统计量的抽样分布为理论依据，按一定概率要求，由样本统计量的值估计总体参数的所在范围。区间估计指出了总体参数落在该范围的概率有多大。

二、置信区间与置信度

置信区间也称置信间距，是指在某一置信度时，总体参数所在的区域距离或区域长度。当要求按某一可靠度（概率）去估计总体平均数的取值区间时，这一可靠度称为置信水平或置信度。犯错误的概率也称为显著性水平，通常用符号表示。例如，置信度为0.95的置信区间是指总体参数落在该区间内，估计正确的概率为95%，而出现错误的概率为5%。置信区间的界限称为置信界限。实践中，常以95%和99%的置信度估计总体参数的置信区间。

三、区间估计的基本原理

区间估计的原理是根据样本统计量抽样分布的理论，用抽样分布的标准误（SE）计算区间长度，并解释总体参数落入某一区间的概率。只有知道了样本统计量的分布规律和抽样分布的标准误，才能对区间估计的概率进行解释。在正确估计的概率即置信度不变的条件下，标准误越小，置信区间的长度越小。一般情况下，使标准误变小的方法是加大样本容量。现以总体平均数的区间估计为例，说明总体参数区间估计的基本原理。

从某正态总体（已知）中随机抽取容量为n的样本，样本平均数的抽样分布为正态分布，抽样分布的平均数为，标准误，每个样本平均数与总体平均数的离差用表示。

查正态分布表可知：

把Z= 代入上面各式并整理得：

即有68.26%的落在之间，有95%的落在之间，有99%的落在之间，如图所示。

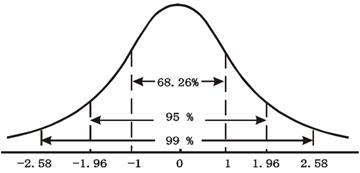
抽样分布的概率

当已知一个样本平均数，可视总体平均数在这个样本平均数的附近波动，并根据一定的概率要求，利用样本平均数来推知总体平均数的区间，即

这样在一定的概率保证下推断出了总体参数的可能范围：出现在之间的可能性为68.26%；出现在之间的可能性为95%；出现在之间的可能性为99%。为置信下限，为置信上限。

其他总体参数的估计原理与总体平均数的估计原理相同，只是要依据不同统计量的抽样分布，而且标准误也不同。

四、区间估计的一般步骤