问题导入学校之所以得出导学案教学方法有效的结论，是因为实验后测试的平均成绩和优秀率高于实验前，从数据上看效果好于之前。但差异的来源有两个，一是抽样误差造成的，二是教学方法不同带来的。分析这所学校得出结论是否合理，就是分析数据之间的差异主要来自哪个方面。如果主要来自抽样误差，则学校的结论不成立；如果主要是由于方法不同造成的，则学校结论成立，这就需要采用假设检验的方法进行分析。

一、统计假设检验的基本思想

假设是根据已有的理论和事实对研究对象所作出的假定性说明。科学研究总是从提出研究假设开始。研究假设是对研究问题的结果即变量之间的关系或研究现象的性质等所作的推测或估计。统计假设检验是指依据一定的原理，利用样本信息，根据一定概率，对总体参数或分布的某一假设作出拒绝或保留的决断。

问题导入中的案例，学校提出如下研究假设：

学校进行教学方法实验的目的是希望新的教学方法比原来的教学方法教学效果好，能够提高学生成绩。在统计假设检验中，此假设称为备择假设，记为。学校是想证明这6分之差是由于教学方法不同引起的，那么我们就假定新的教学方法对学生学习成绩提高没有效果，这6分之差是由抽样误差造成的，然后检验这一假设的正确性。这是要一个与相反的假设，称为虚无假设或原假设、零假设，记为。统计假设检验要提出两个假设，原假设和备择假设，这两个假设必需互斥和穷尽。不能作为被直接检验的假设，是作为直接被检验的假设。假设检验的问题，就是判断是否正确。如果通过统计方法证明正确，则接受原假设，拒绝备择假设；否则拒绝原假设，接受备择假。因此，这两个假设只有一个是正确的，而原假设是统计推断的出发点。著名统计学家费舍曾指出：“可以说，每一个实验的存在，仅仅是为了给事实一个反驳虚无假设的机会。”

所以统计假设检验的逻辑思想是：先假设成立，然后通过样本收集实际信息，在原假设条件下依据抽样分布理论进行数学上的计算、分析，并依据正确的逻辑进行推理，看实际获得的资料所导致的结果与原假设成立时应出现的结果是否一致。如果实际发生的结果与原假设成立前提下的结果出现了矛盾，则有理由认为原假设是错误的，应该给予否定，从而接收备择假设；如果没有出现矛盾，则没有充分理由否定原假设，也就没有充分理由接受备择假设。

判断是否成立的依据是小概率原理。小概率事件发生的概率越小，说明实际获得信息反映出的结果与成立下推论的结果之间矛盾越明显，实际结果与原假设结果的差异越显著，越有理由拒绝原假设，接受备择假设。因此，统计假设检验也称为显著性检验。判断差异显著与否的标准是小概率事件发生的水平，称为显著性水平，用（ 读alpha)表示，假设检验中通常取0.05或0.01。在0.05水平是拒绝原假称为差异显著，在0.01水平是拒绝原假称为差异非常显著。一般情况下，如果计算的检验统计量能在0.01水平上拒绝原假设，就不在0.05水平上拒绝；能在0.05水平上拒绝原假设，就不在0.01水平上接受原假设。α水平所对应的样本抽样分布的边界值为临界值。因此，统计假设检验是依据抽样分布理论和确定的数量标准（显著性水平和临界值），采用反证法来判断假设是否成立，并能估计判断结果的可靠性。

二、统计假设检验中的两种方式

显著性水平由研究者根据实际情况或问题需要确定，大多数情况通常取0.05或0.01。显著性水平一旦确定，则拒绝原假设的界限值就会确定。由于对要检验的两个量数间差异的方向了解程度不同，或关心的问题不同，检验时，水平这个小概率有时置于抽样分布的一侧，有时置于分布的两侧，这就使检验方式分为单尾检验和双尾检验两种。

（一）双尾检验

如果研究人员对于两总体参数间差异的方向无法得知或根本不关心，只关心其差异的绝对值，则采用双尾检验，显著性水平被平均分配在抽样分布的双尾，即拒绝原假设的区域分布在抽样分布的两尾端，如平均数差异检验的假设为：：=；：≠。

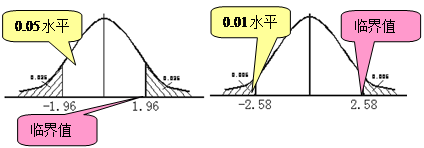
如在正态分布情况下，采取Z检验法，如果选取水平为0.05，采用双尾检验，0.05平分在双尾，各为0.025，而界限值为=±1.96。这时统计量无论从左边还是从右边达到或超过界限值，都可在该水平上拒绝原假设。=0.01时的双尾界限值为=±2.58。中间为接受区，两尾阴影部分为拒绝区。
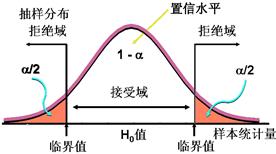
如果显著性水平为，则接受区与拒绝区如下图所示。

（二）单尾检验

如果在检验前依据某些理论或经验已知其中一总体参数大于或小于另一总体参数，这时，研究者不但关注参数之间是否存在差异，还关注差异方向。如问题导入中，学校教改的目的是希望导学案教学效果优于原来的教学效果，这时采用右单尾，假设为：

:，: >

有的时候需要左单尾检验，假设为：:，:<。

在Z检验中，显著性水平为0.05，右单尾检验时，由实际观测值计算的两统计量差异如果达到或超过1.64（左单尾值为-1.64），则在0.05水平上拒绝的假设，否则接受它。如果取0.01水平，则右尾界限值为2.33（左单尾值为-2.33），图的阴影部分为拒绝区。

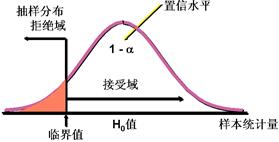
如果显著性水平为，左单尾检验的接受区与拒绝区为：

一般情况下，适合用单尾检验的，应采用单尾检验的方式。因为相同水平下，单尾检验的临界值要小于双尾临界值，拒绝假设的机会加大。如果此时用双尾检验，实际上等于提高了显著性的水平（），但结论仍按原显著水平作出，使信息受损。在实际研究中，常由于变量间差异方向不清，所以使用双尾检验的情况较多。