第五章 统计假设检验(上)
 知识点二:假设检验中的两类错误和一般步骤
知识点二:假设检验中的两类错误和一般步骤
一、假设检验中的两类错误
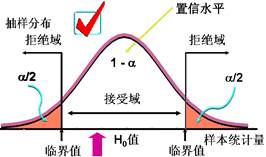
用样本去推断总体,由于抽样误差的存在,是在一定的概率水平下进行的,不可能有百分之百的把握肯定无误。假设检验时,只是依样本统计量出现的概率的大小来决定假设的取舍,这样就有四种可能结果:接受了正确的假设;拒绝了错误的假设;接受了错误的假设;拒绝了正确的假设。前两种结果是正确的,是统计假设检验希望实现的,后两种结果是错误的,是假设检验不愿意发生的。
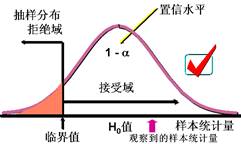
当显著性水平为0.05时,如果![]() 假设是正确的,按抽样分布的理论来说,根据实际样本值计算的统计量Z值应有95%的把握落在|Z|<1.96之内,而落在|Z|≥1.96的可能性只有5%。如果实际计算的统计量Z值真的落在|Z|<1.96之内,则接受
假设是正确的,按抽样分布的理论来说,根据实际样本值计算的统计量Z值应有95%的把握落在|Z|<1.96之内,而落在|Z|≥1.96的可能性只有5%。如果实际计算的统计量Z值真的落在|Z|<1.96之内,则接受![]() 假设而得出正确的结论。但是由于样本的随机性,样本统计量也是随机变量,有时尽管
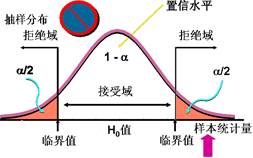
假设而得出正确的结论。但是由于样本的随机性,样本统计量也是随机变量,有时尽管![]() 假设是正确的,而实际获得的样本统计量之值也有可能落入拒绝区。这是因为按抽样分布的理论,样本统计量的值确实有5%分布在拒绝区,尽管这个概率很小,但不是不存在。如果原假设本来正确而统计量却落在拒绝区,我们依此拒绝
假设是正确的,而实际获得的样本统计量之值也有可能落入拒绝区。这是因为按抽样分布的理论,样本统计量的值确实有5%分布在拒绝区,尽管这个概率很小,但不是不存在。如果原假设本来正确而统计量却落在拒绝区,我们依此拒绝![]() ,就得出了错误结论。此时我们犯的是一种弃真的错误,统计上称这种错误为第一类错误,也叫
,就得出了错误结论。此时我们犯的是一种弃真的错误,统计上称这种错误为第一类错误,也叫![]() 错误。统计推论时犯第一类错误的概率等于显著性水平
错误。统计推论时犯第一类错误的概率等于显著性水平![]() ,
,![]() 值越大,犯第一类错误的可能性越大。
值越大,犯第一类错误的可能性越大。
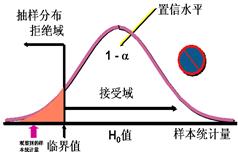
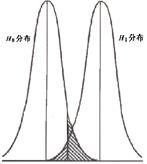
单尾检验,![]() 正确时,样本统计量落在接受区和拒绝区的情况为:
正确时,样本统计量落在接受区和拒绝区的情况为:
另外一种情况是,![]() 假设是错误的,经检验被拒绝,这样得出了正确的的结论。然而,由于样本统计量的随机性,尽管
假设是错误的,经检验被拒绝,这样得出了正确的的结论。然而,由于样本统计量的随机性,尽管![]() 是错误的,但实际获得的样本统计量也有可能落入接受区而使我们接受了
是错误的,但实际获得的样本统计量也有可能落入接受区而使我们接受了![]() 假设,得出错误的结论。此时我们犯的是一种存伪的错误,统计上称为第二类错误,也叫
假设,得出错误的结论。此时我们犯的是一种存伪的错误,统计上称为第二类错误,也叫![]() (读Beta)错误。犯第二类错误的概率用
(读Beta)错误。犯第二类错误的概率用![]() 表示。
表示。
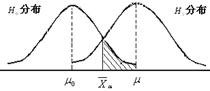
在两类错误中,由于![]() 错误比较好估计,它出现的可能性与选取的显著性水平相当,例如检验中选取的水平为0.05,那么犯第一类错误的机会就是0.05。而影响错误的因素主要有:显著性水平
错误比较好估计,它出现的可能性与选取的显著性水平相当,例如检验中选取的水平为0.05,那么犯第一类错误的机会就是0.05。而影响错误的因素主要有:显著性水平![]() ,当
,当![]() 减少时增大;总体标准差
减少时增大;总体标准差![]() ,当
,当![]() 增大时增大;样本容量
增大时增大;样本容量![]() ,当
,当![]() 减少时增大。因此在实际研究中,人们常采取三种方法控制两类错误的概率。一是选取适当的水平,通常取0.1,0.05,0.01,0.025,0.001 等数值,具体视研究问题的性质而定。在社会科学研究中常取0.05;二是利用已知的被比较的两个量数间的大致关系,合理安排单尾或双尾检验;三是适当增加样本容量,减少随机误差,尽量降低两类错误的概率,或者一个减少,不致于使另一个增加。例如样本平均数抽样分布的标准误为
减少时增大。因此在实际研究中,人们常采取三种方法控制两类错误的概率。一是选取适当的水平,通常取0.1,0.05,0.01,0.025,0.001 等数值,具体视研究问题的性质而定。在社会科学研究中常取0.05;二是利用已知的被比较的两个量数间的大致关系,合理安排单尾或双尾检验;三是适当增加样本容量,减少随机误差,尽量降低两类错误的概率,或者一个减少,不致于使另一个增加。例如样本平均数抽样分布的标准误为![]() ,当n增大时样本平均数分布将变得陡峭,在
,当n增大时样本平均数分布将变得陡峭,在![]() 其他条件不变时
其他条件不变时![]() 会减少。
会减少。
二、统计假设检验的一般步骤
1.建立假设。根据实际情况选择检验方式后建立![]() 和
和![]() 。
。
2.选择和计算统计量。根据数据的特点,选择合适的抽样分布和统计量,并计算统计量的值。常用抽样分布有正态分布、t分布、![]() 分布、
分布、![]() 分布等。与各种分布相对应的检验方法分别为
分布等。与各种分布相对应的检验方法分别为![]() 检验、
检验、![]() 检验、
检验、![]() 检验、
检验、![]() 检验等,计算统计量就是求
检验等,计算统计量就是求![]() 值、
值、![]() 值、
值、![]() 值或
值或![]() 值。
值。
3.确定显著性水平和临界值。依据需要确定显著性水平![]() ,查相应的统计用表,确定
,查相应的统计用表,确定![]() 水平下的临界值,即
水平下的临界值,即![]() 的接受区间和拒绝区间。
的接受区间和拒绝区间。
4.判断结果并解释。检验结论由计算出的统计量值与查表得到的某显著水平下的临界值相比较而得出。如果计算的统计量值达到或超过临界值,则拒绝![]() ,接受
,接受![]() 。如
。如![]() 检验中,若计算的统计量|
检验中,若计算的统计量|![]() |≥
|≥![]() 或|
或|![]() |≥
|≥![]() 时,便有理由拒绝
时,便有理由拒绝![]() 假设,接受
假设,接受![]() ,说明比较的两个量数之间差异显著;否则接受
,说明比较的两个量数之间差异显著;否则接受![]() 假设,认为差异不显著,差异主要来源于抽样误差。
假设,认为差异不显著,差异主要来源于抽样误差。
