问题导入中分析实验后36名学生的样本平均数与学校原有的总体平均数之间的差异，实际上分析的实验后新的总体平均水平与原有总体平均水平之间的差异，这就是单总体平均数假设检验，即对样本统计量与已知总体参数之间的差异所进行的显著性检验。经过检验，如果样本统计量与相应总体参数差异显著，说明该样本已不属于已知总体；如果差异不显著，说明样本统计量与已知总体参数之间的差异主要来源于抽样误差。我们主要学习总体平均数与总体比率的检验方法。

一、总体平均数的显著性检验

总体平均数的显著性检验是指对样本平均数与已知总体平均数间的差异进行的显著性检验。若检验的结果差异显著，表明样本平均数与总体平均数的差异不能认为完全是由抽样误差造成的，可以认为来自另外一个总体。否则，认为来自平均数为的总体，差异主要是由抽样误差造成的。根据总体的分布形态、总体方差是否已知及样本大小等情况，平均数的显著性检验可采用不同的检验方法。

（一）总体正态分布，总体方差已知

问题导入中的案例就是这样的情况。此时无论样本大小，均采用检验。检验公式为：

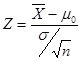
式中，为样本平均数；为总体平均数；为总体标准差；为样本容量。

检验的统计决断规则是：

以问题导入中的案例为例，说明检验的方法：

（1）确定检验形式，提出虚无假设和备择假设。: : >

（2）计算值。

=

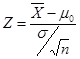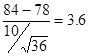
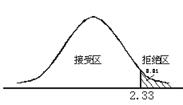
（3）确定显著性水平和临界值。

取=0.01，右单尾检验的临界值是。

（4）统计决断。所计算的值与一定显著性水平下的临界值相比较，得出结论。

由于计算的＞2.33，P＜0.01，因此，拒绝原假设，认为导学案的教学效果明显好于该校原来教学方法的教学效果。

（二）总体正态分布，总体方差未知

1.大样本时

这时样本平均数的抽样分布服从或近似正态分布，检验样本平均数与总体平均数间的差异用检验，可作为总体标准差的估计值，公式为：

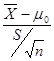
如某地区调查表明，该市幼儿大班儿童的平均身高为116.5cm。某调查组从该市的一所幼儿园中随机抽取50名大班幼儿，测得他们的身高如下。问该幼儿园大班幼儿的平均身高是否与全地区大班幼儿的平均身高一致？119，120，118，129，109，120，117，100，119，120，131，119，99，122，108，110，138，130，122，108，135，111，125，115，98，106，118，116，121，110，105，113，109，112，107，134，94，100，124，128，118，123，125，99，114， 115，120，99，127， 140
解：：=，：≠

=116.38，S=10.87，-0.078

取α=0.05，查正态分布表得0.05/2=1.96。由于计算的=0.078 <0.05/2=1.96，P>0.05，所以接受原假设，认为该幼儿园大班幼儿的平均身高与全地区大班幼儿的平均身高一致，差异主要是由偶然因素造成的。

2.小样本时

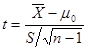当小样本时，作为总体标准差的估计值。样本平均数抽样分布的标准误为，服从自由度为的分布，所以要检验小样本平均数与总体平均数的差异是否显著，须采用检验，公式为：或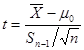       

t检验的步骤和检验一样，统计决断的规则为：

与临界值的比较	P值	检验结果
< ≤< ≥	P>0.05 0.01<P≤0.05 P≤0.01	接受，拒绝 在0.05水平上拒绝，接受，差异显著 在0.01水平上拒绝，接受，差异非常显著

如某小学上届三年级学生学习能力测试平均成绩=76分，这一届三年级20个学生的学习能力测试的平均成绩为=82分，标准差为=10.4分。假定这一届学生与上届学生学习条件和环境相同，试分析这一届三年级学生的学习能力是否好于上一届学生？

解：: ，: >

由于=20<30，总体标准差未知，所以适用于检验。

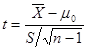
=2.51

根据题意及假设的形式，取α=0.05，自由度=20-1=19。查分布表，=1.729。

由于计算的=2.51>=1.729，P<0.05，所以在0.05水平上拒绝原假设，接受备择假设，结论为：这一届三年级学生的学习习惯比上一届学生的学习习惯好。

（三）总体非正态分布

数学上已证明，无论总体是否正态，随着的增大，样本平均数的分布皆趋于正态或近似正态分布。所以，无论总体是否正态，只要n>30，检验样本平均数与总体平均数之间的差异，可以采用检验。

二、总体比率的显著性检验

问题引入中，实验前学生的优秀率为28%，实验后36名学生的优秀率达到35%，提高了7%。但提高的百分比是不是主要由教学方法改变带来的，需要经过检验才能确定。这就是总体比率的假设检验。

比率的抽样分布是二项分布。用作为样本成功事件的概率，当时，二项分布呈对称分布；当>且≥5（或<且≥5）时，二项分布接近正态分布。因此，总体比率的假设检验可用检验，公式为：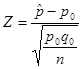
式中，为已知总体中事件A发生的概率；；为样本容量；。

问题引入中优秀率的检验过程为

（1）提出假设。: =，:

（2）选择统计量并计算其值。将=0.281，=1-0.28=0.72，=0.35，=36带入公式得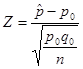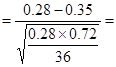：-0.935

（3）确定显著性水平和临界值。α=0.05，=1.96

（4）统计决断。由于计算的=0.935<0.05/2=1.96，P>0.05，因此，保留原假设，实验后学生成绩的优秀率与实验前差异不显著。