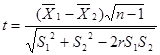第五章 统计假设检验(上)
 知识点四:两个样本平均数间差异的显著性检验
知识点四:两个样本平均数间差异的显著性检验
考试分数是评价培训中心教学质量差异的主要因素。管理部门为了考察两个培训中心的教育质量,在两个培训中心各随机抽取接受过培训的学员参加考试。随机抽取A培训中心培训过的学员35名,平均成绩为![]() =83.2分,在B培训中心接受过培训的学员40名,平均成绩为
=83.2分,在B培训中心接受过培训的学员40名,平均成绩为![]() =78分。根据以往资料可知A培训中心学员成绩的标准差为
=78分。根据以往资料可知A培训中心学员成绩的标准差为![]() =8,B培训中心学员成绩的标准差为
=8,B培训中心学员成绩的标准差为![]() =10,成绩服从正态分布。试分析两个培训中心的教育质量是否存在差异。
=10,成绩服从正态分布。试分析两个培训中心的教育质量是否存在差异。
这一问题是通过比较![]() 与
与![]() 之间的差异,来说明它们所来自的两个培训中心教学质量间是否存在差异。两个样本平均数间差异的显著性检验,就指根据两个样本平均数之间的差异(
之间的差异,来说明它们所来自的两个培训中心教学质量间是否存在差异。两个样本平均数间差异的显著性检验,就指根据两个样本平均数之间的差异(![]() -
-![]() )来检验两个相应总体平均数之间差异(
)来检验两个相应总体平均数之间差异(![]() -
-![]() )是否显著。原理与单总体平均数显著性检验一样,首先提出假设(H0:
)是否显著。原理与单总体平均数显著性检验一样,首先提出假设(H0:![]() =
=![]() ,H1:
,H1:![]() ≠
≠![]() ),然后以两个样本平均数之差的抽样分布为理论依据,来考察两个样本平均数之差是否来自两个总体平均数之差为0的总体。如果两个样本平均数之差在其抽样分布上出现的概率足够小,达到了一定的显著性水平,则拒绝零假设,接受备择假设,得出两个总体平均数间有本质差异的结论;否则接受原假设,两个样本平均数之差主要由抽样误差引起的。
),然后以两个样本平均数之差的抽样分布为理论依据,来考察两个样本平均数之差是否来自两个总体平均数之差为0的总体。如果两个样本平均数之差在其抽样分布上出现的概率足够小,达到了一定的显著性水平,则拒绝零假设,接受备择假设,得出两个总体平均数间有本质差异的结论;否则接受原假设,两个样本平均数之差主要由抽样误差引起的。
两个平均数间差异的显著性检验既要考虑总体分布与总体方差,同时要注意方差是否齐性,以及两个样本是否相关等条件。
一、两个独立样本平均数间差异的显著性检验
独立样本是指随机抽取的两个样本之间没有关系。要检验这样的两个样本是否来自相同的总体,可根据不同的情况采取不同的检验方法,但前提是样本所来自的两总体方差齐性。方差齐性也叫方差相等,是指两方差间差异不显著。这是因为,两总体方差不相等,其平均数的代表性就不同,这时平均数进行相互比较,其结果的可靠性就受到影响。方差是否齐性,需要经过方差齐性检验(详见知识点六)。
(一)总体正态分布,总体方差已知、齐性
此时两样本平均数之差的分布为正态,无论样本大小,均适用于![]() 检验。公式为:
检验。公式为: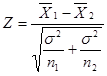
式中,![]() 、
、![]() 分别是两个样本的平均数;
分别是两个样本的平均数;![]() 、
、![]() 分别是两个样本来自的总体的方差;
分别是两个样本来自的总体的方差;![]() 、
、![]() 分别为两个样本的容量。
分别为两个样本的容量。
两个培训中心教学质量是否存在差异检验如下:
(1)提出假设。H0:![]() =
=![]() ,H1:
,H1:![]() ≠
≠![]()
(2)计算Z值。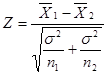 =
=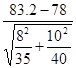 =2.499
=2.499
(3)确定α水平及临界值。选取显著性水平为α=0.05,查正态分布表,Z0.05/2=1.96。
(4)统计决断。由于计算的Z=2.499>Z0.05/2=1.96,P<0.05,所以在α=0.05上拒绝原假设,接受备择假设,结论为两个培训中心的教育质量存在差异。
(二)总体正态分布,总体方差未知但齐性,两个样本容量均大于30
此时两个平均数之差的分布为正态或近似正态,用样本方差直接代替总体方差,采用![]() 检验。公式为:
检验。公式为: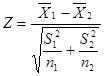
式中, ![]() 、
、![]() 分别是两个样本的方差;
分别是两个样本的方差;![]() 、
、![]() 分别为两个样本的容量。
分别为两个样本的容量。
(三)总体正态分布、总体方差未知、齐性,样本容量小于30
当总体方差未知但相等,两个样本容量n1和n2均小于30,或其中一个小于30时,平均数间差异的显著性检验用![]() 检验,公式为:
检验,公式为: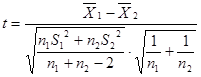
式中,![]() 、
、![]() 分别是两个样本的平均数;
分别是两个样本的平均数;![]() 、
、![]() 分别是两个样本的方差;
分别是两个样本的方差;![]() 、
、![]() 分别为两个样本的容量。
分别为两个样本的容量。
如某老师为了研究在高中阶段“男生”与“女生”学习数学方面存在的差异,把全班52名学生的数学成绩按男生和女生进行分类统计。全班28名男生的平均成绩为70.4分,标准差为10.6分;24名女生的平均成绩为66.8分,标准差为9.4分。问李老师怎样评价高中阶段“男生”与“女生”数学成绩方面存在的差异?
解:男、女生虽组成一个教学班,但成绩是按男、女生分别统计的,这实际上就形成了从两个正态总体中随机抽取的独立样本。“男生”与“女生”的平均成绩存在一定的差异,但差异是由于抽样误差造成的,还是因为性别对数学成绩有实质性影响,采用![]() 检验法检验差异的来源。
检验法检验差异的来源。
H0:![]() =
=![]() ,H1:
,H1:![]() ≠
≠![]()
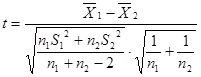 =
=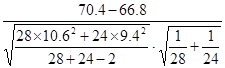 =1.26
=1.26
取α=0.05,df =![]() +
+![]() -2=28+24-2=50。查t值表,得t0.05/2(50)=2.01。
-2=28+24-2=50。查t值表,得t0.05/2(50)=2.01。
由于计算的t=1.26< t0.05/2(50)=2.01,所以接受原假设,拒绝备择假设,说明“男生”与“女生”在平均分上的差异主要是由于抽样误差造成的,即“男生”与“女生”的真实水平并无差异。所以,在教学中认为男生数学水平比女生数学水平高的看法是片面的、缺乏科学依据的。
二、两个相关样本平均数间差异的显著性检验
相关样本是指两个样本内个体之间存在一定的关系,有两种情况:一是同一组被试在不同条件下形成的两组样本间存在相关。如用同一份测验对同一组被试在实验前和实验后进行两次测验,所获得的两组测验结果是相关样本。二是在成对匹配的两组被试条件下形成的样本存在相关。如将被试按某种原则一一配对,然后每对被试随机地分入实验组和对照组,对两组被试施以不同的实验处理之后,用同一个测验所获得的测验结果是相关样本。
由于相关样本的相关程度对实验结果有一定影响,因此对相关样本间差异进行检验时要考虑相关程度。另外,对两总体方差是否相等不做要求。根据方差是否已知及样本大小,采用不同的检验方法。
(一)总体正态分布,总体方差已知
此时,不管大小样本,都采用![]() 检验,公式为:
检验,公式为: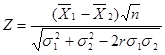
式中,![]() 、
、![]() 分别是两个样本的平均数,
分别是两个样本的平均数,![]() 、
、![]() 分别是两样本来自的总体的标准差;
分别是两样本来自的总体的标准差;![]() 为成对观测值个数;
为成对观测值个数;![]() 为两样本间的相关系数
为两样本间的相关系数
(二)总体正态分布,总体方差未知,![]() >30
>30
此时,仍采用![]() 检验,用样本方差代替总体方差,公式为:
检验,用样本方差代替总体方差,公式为: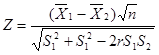
式中, ![]() 、
、![]() 分别是两样本的标准差
分别是两样本的标准差
如从某实验学校三年级中随机抽取47名学生,进行阅读能力训练。训练前进行一次测验,测验结果的平均成绩为71分,标准差为8.2分。训练两个月后,又采用等值测验进行测试,平均成绩为76分,标准差为9.6分,两次测验的相关系数为0.53。问阅读能力训练对提高学生的阅读能力是否有促进作用?
解:提出假设。设训练前的平均成绩所来自的总体平均数为![]() ,训练后的平均成绩所来自的总体平均数为
,训练后的平均成绩所来自的总体平均数为![]() ,采取右单尾检验。H0:
,采取右单尾检验。H0:![]()
![]()
![]() ,
,![]() :
:![]() >
>![]()
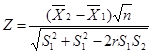
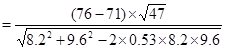 =3.93
=3.93
取α=0.01,查正态分布表,右尾检验的临界值Z0.01=2.33
由于计算的![]() =3.93>Z0.01=2.33,所以在0.01水平上拒绝原假设,接受备择假设。结论为训练前后两次测验的平均成绩差异非常显著,训练后学生进步很大,阅读训练对提高学生的阅读能力有较大的促进作用。
=3.93>Z0.01=2.33,所以在0.01水平上拒绝原假设,接受备择假设。结论为训练前后两次测验的平均成绩差异非常显著,训练后学生进步很大,阅读训练对提高学生的阅读能力有较大的促进作用。
(三)总体方差未知,![]() <30
<30
此时适用于![]() 检验,
检验,![]() =n-1。计算统计量t值的公式为:
=n-1。计算统计量t值的公式为: