两个比率间差异的显著性检验是检验两个相应总体的比率是否有显著性差异。如果两个比率、分别表示两个独立样本中同一事件发生的比率，且≥5，≥5，则两个样本比率之差的抽样分布服从或接近于正态，可用Z检验法来检验两个比率之间差异的显著性。公式为：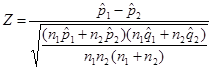 

式中，、分别为两样本中某事件发生的比率；、为两样本容量；=1-，=1-。

如某教育局在考察全面贯彻党的教育方针的情况时发现，经常参加课外活动（如文艺社团、科技小组、体育竞赛等）的学生，在甲校占64%，在乙校占58%，试问两校参加课外活动的人数有无显著性差异？

解：H0：=，H1：≠

由于题中没有给出两校学生的各自容量，根据题意，学校学生的容量不可能小于30，为了计算简便，设n1=100，n2=100，计算相关的值：

两校参加课外活动的人数

所以，=1-=1-0.64=0.38，=1-=1-0.58=0.42

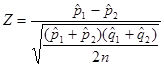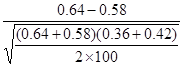==0.87

取=0.05。由于计算的Z=0.87<Z0.05/2=1.96，所以接受原假设，认为甲乙两校参加课外活动的人数比率间差异不显著。

凡是以二分变量为标度的两个独立样本，只要n>30，检验样本比例间差异显著性均可用此方法。所以这种检验方法在教育、教学中应用广泛。