两个独立样本平均数间差异的显著性检验的条件之一就是被检验的总体方差齐性。比较两个以上平均数间差异是否相等的条件之一也是被比较的多个独立样本的方差要相等。要知道多个样本来自的相应总体方差是否相等，就要进行方差的显著性检验。统计上检验两个或多个独立样本的方差差异是否显著，采用的是F检验。

一、F分布与F检验

F检验以及方差分析都是依据F分布。F分布是一种小样本的分布，在实践中有广泛的用途，其自由度为（n1-1、n2-1），计算公式为：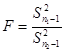

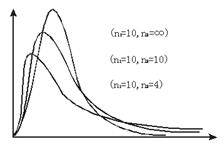
F分布是随着分子自由度和分母自由度变化而变化的一簇单峰偏态分布曲线，所以曲线两尾的F值不对称。F分布附表列出了自由度为dƒ1、dƒ2的F分布的F0.05、F0.01的F临界值，附表的最上端横行表示F比值中分子的自由度dƒ1，最左端纵列表示分母的自由度dƒ2，表中概率为p（F>Fα）=α，即F分布右尾端的概率（单尾值）。而左尾端的F1-α值，理论上指出是右尾Fα值的倒数，其概率为1-α。一般情况下，计算F值时，把较大方差做分子，较小方差做分母，即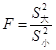

F检验是进行方差齐性检验的主要工具，就是利用两方差之比，即与理论推算的F值表上相应数值进行比较，以判断两方差差异的大小。它主要检验两个或两个以上独立样本方差是否相等。其统计决断规则为：

二、两个独立样本方差间差异的显著性检验

我们假定X1，X2，…，Xn是从正态总体X中随机抽取的容量为n1的样本，Y1，Y2，…，Yn是从正态总体Y中随机抽取的容量为n2的样本，其方差分别为和。如果假设H0：=为真，则和应相差无几，即应与1相差不多，这样两样本来自方差相同的总体；如果由观测值计算的F值与1相差很大，大于一定α水平的F分布理论临界值，即当F>Fα时，则拒绝原假设，认为两样本来自的两总体方差差异显著。由于F分布是不对称的，因此，相同α水平下的左右尾的F值不同。同时把较大的方差做为分子，较小的方差做为分母，所以，在实际应用中常用右尾值进行显著性检验。

如某老师新接初三两个班的英语课。从上学期期末考试结果中该老师了解到两个班的英语成绩不太理想。一班52人，平均成绩为72分，标准差为12.1分；二班58人，平均成绩也是74分，标准差为5.4分。问这两个班英语成绩的离散程度是否相同？

解：H0：，  H1：>

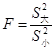==5.021

取=0.01，根据dƒ1=n1-1=52-1=51，dƒ2=n2-1=58-1=57，查F值表。由于表中分子自由度没有51、分母自由度没有58，因此，在F值表选择最接近该分子、分母自由度的一项，得得F0.01（51，57）=1.87

由于实际计算出的F=5.021< F0.01（51，57）=1.87，P>0.01。根据F检验统计决断规则，在0.01水平上拒绝原假设。结论为，这两个班的英语成绩的离散程度不相同，一班学生成绩波动要比二班学生成绩波动大。

三、多个独立样本方差差异的显著性检验

在教育管理中，经常涉及到比较多所学校学生成绩的离散程度是否一致、同一学科几个班级考试成绩的波动情况是否一致等。这就涉及多个样本方差差异的显著性检验，最常用的方法是哈特莱最大F值检验法。它是以各样本方差中最大者和最小者之比求得最大F值，然后检验此值是否达到一定显著性水平下的理论F界限值。

确定临界值时根据自由度和要比较的方差的个数k查的临界值表，如果大于或等于理论F界限值，则认为各总体方差不齐性，否则接受原假设，认为各样本所来自的总体方差齐性。公式为：

 

式中，为各样本方差中数值最大者；为各样本方差中数值最小者。

如某乡镇从五所小学中各随机抽取一部分四年级学生，参与语文水平测试，其测验结果如表所示。问各校语文测验成绩的离散程度是否一致？

五所学校语文测验成绩

解：（1）提出假设。H0：====，H1：至少有两个总体方差不等

（2）计算值。依据样本实际观测值，求得各校语文成绩的方差：=46.92，同理，=55.21，=51.27，=30.91，=151.54。因为方差中最大者为=151.54，最小者为=30.91，所以：
4.75

（3）确定显著性水平，并查表。表中k为被比较的方差的个数，自由度为df=n-1。本例k=5，df=n-1=7-1=6。取α=0.05，查表得0.05=12.1。

（4）统计决断。因为实际计算的=4.75<0.05=12.1，所以保留原假设，结论为：五所学校的语文成绩的离散程度是一致的。

上例是各组方差n相等的情况。当各组容量n不相等时，方差齐性检验的方法和步骤同n相等时一样，只不过确定自由度时，用容量最大的一组的n计算自由度，然后查表，确定临界值，进行统计决断。