一、方差分析的概念

某校用学生期末考试的平均成绩评价教师的教学业绩。五年级共5个班，数学课分别由五位教师担任，学校应该采用什么方法对五个班的平均成绩进行比较，以确定教师教学业绩的高低。我们学过的Z检验和t检验是对两个平均数间差异的显著性检验，要综合比较三个或三个以上平均数之间的差异，以确定自变量对因变量的影响程度，Z检验、t检验就不适合了。这时要用方差分析的方法，即通过F检验实现对多个平均数间差异的综合比较。

方差分析也称作变异数分析，是把总变异分解为几个变异，即把引起方差变化的各种因素进行统计分析、比较，进而检验出形成各样本差异的主要原因（或因素），并与规定的理论F值比较，以判断平均数间差异是否显著。

二、方差分析的逻辑思想

随机抽取了三所学校各4名学生的语文统考成绩，不同类型学校的考试成绩有很大差异，同时全部观测值间也参差不齐。

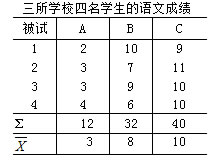
造成这种差异的原因是多方面的，有些可能是由各组平均数的差异（学校的水平不同），即组间差异产生，如=3分，=8分，=10分，三个组的平均水平有高有低；有些可能是由随机抽样误差及其它未知的原因，即组内差异所造成，如第二组最高分10分，最低分为6分，这种差异是各学校的内部差异。

方差分析的基本原理就是首先将总体变异分解为样本组间变异和由抽样误差等其它原因产生的组内变异，然后分析变异各组成部分的关系。如果样本组间变异（方差）比组内变异显著地大，大于或等于一定显著性水平的F临界值，则认为样本组间有实质性的差异，如三所学校办学水平差异显著；如果样本组间变异与组内变异相比较差异不大，没有达到一定显著性水平的F临界值，那么有理由认为样本组间没有实质性差异，如三所学校办学水平一致。所以要想了解数据之间的差异状况，需将这些数据与总体平均数之间的差异进行分析。方差分析的逻辑就是通过组间和组内的方差之比（即F值）来实现对几个平均数间差异的显著性检验，方差的可加性是其基本理论依据。

方差分析中，观测值之间的差异情况用离差平方和表示，符号为SS。方差分析首先把总体平方和分解为组间平方和与组内平方和，即：                                    

式中，SSt为总平方和；SSb为组间平方和；SSw为组内平方和

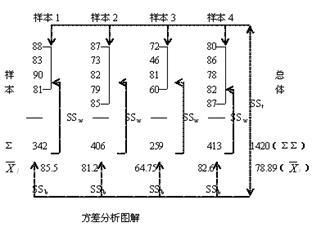
我们以问题引入中的例子来说明总平方和、组间平方和、组内平方和及三者之间的关系。分析不同版本的教材对学生学习成绩的影响是否相同，就是检验四个班的平均数是否有显著性差异，这就需要分析四个班学生的组间差异和每班学生的组内差异及二者的关系。

总体平方和SSt是总体中各观测值与总体平均数间的离差平方和，即

SSt=(88-78.89)2+(83-78.89)2+……+(81-78.89)2=1993.778

组间平方和SSb是指各样本平均数与总体平均数间的离差平方和，即

SSb=4(85.5-78.89)2+6(81.2-78.89)2+……+5(82.6-78.89)2=1070.028

组内平方和是指组内每个观测值与本组平均数间的离差平方和，即：

SSw=(88-85.5)2+……+(87-81.2)2+……+(72-64.75)2+……+(80-82.6)2+……=923.75

从结果中可看出1993.778=1070.028+923.75，即。这一等式也表明了总平方和、组间平方和、组内平方和之间的关系：当总体平方和一定时，SSb越大，SSw就越小，反之亦然，这是差分析的理论基础。如果用表示实验中的各个分数，表示第组的平均数，表示总体平均数，则SSt、SSb、SSw可表示为：

，   ，

式中，为各观测值；为第个样本的平均数；为总体平均数；为第个样本的容量；=1、2、…（为样本容量）；=1、2、…（为样本个数）

总体自由度也可分解为组间自由度和组内自由度：

总体自由度为:=nk-1=N-1；

组间自由度：=样本个数-1=k-1；

组内自由度： =(n1-1)+(n2-1)+……+(nk-1)=N-k；(n不相等时)

问题引入中例子的自由度分别为：=18-1=17，=4-1=3；=18-4=14

当总体差异一定时，如果组间差异小于组内差异，说明各组平均数间差异较小，此时各小组实验条件之间的差异对研究样本影响不大，实验效果不明显；反之，则说明各组平均数间差异很大，此时，实验效果明显。但平方和是累加而成的，其大小与数据个数和样本数目有关。因此，要考虑到各自的自由度，即求组间方差和组内方差。在方差分析中，方差一般被称为均方，用表示。组间平方和与组内平方和分别除以各自的自由度，则得到组间均方和组内均方，即：，

式中，为组间均方；为组内均方

组间均方与组内均方是相互独立的，可用F值来检验组间均方与组内均方是否相等。由于研究者关心的是组间均方是否显著地大于组内均方，如果组间均方小于组内均方，则无需检验。因此，将组间均方放在分子位置，进行单侧检验，即。如果计算的F值很大，达到或超过了F抽样分布上某种显著性水平的临界值，则认为组间均方与组内均方有显著性差异，总体差异主要由组间差异造成的。

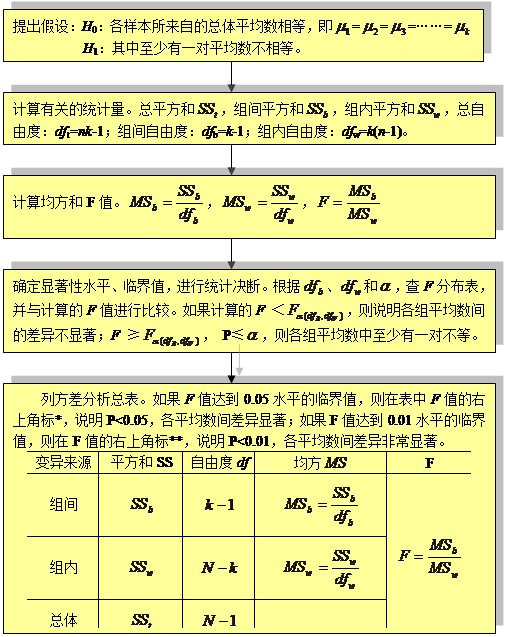
多个平均数间差异显著性检验的原假设为：各样本所来自的总体平均数相等；备择假设为：其中至少有一对平均数不等。检验时，按组间自由度（）和组内自由度（）查

F分布表，找到（，），然后把计算的F值与理论临界值进行比较，进而做出决断。如果计算的F<，则接受原假设，认为各平均数间差异不显著，其差异主要是由随机因素造成的，检验结束；如果计算的F≥，则拒绝原假设，接受备择假设，说明多个平均数并非来自同一总体，至少有一对是不相等的。
问题引入中的=，=，=。取，。由于计算的=5.40＞3.34，所以拒绝原假设，接受备择假设，认为这4个班级至少有一对平均数不等。

二、方差分析的一般步骤    

三、方差分析的基本条件

1．变异的可加性。这是进行方差所依据的基本原理。方差分析中要求将总体变异分解成几部分，这几部分变异的来源意义要明确。同时，由于被试分组是随机分配，个体差异及实验误差带有随机性质，因此，变异间相互独立。

2．总体服从正态分布。在进行方差分析时，要求各样本来自的总体正态分布。教育中的众多现象都服从正态分布，一般情况下可不作正态性检验。

3．方差齐性。进行方差分析时，要求各样本来自的总体方差相等。因此，在进行方差分析之前，一般要用哈特莱最大F值对样本方差进行齐性检验，以便确定能否进行方差分析。